题目内容
17.函数$f(x)=\left\{{\begin{array}{l}{{{(\frac{1}{2})}^x}\;,x≥4}\\{f(x+1)\;,x<4}\end{array}}\right.$,则f(log23)=( )| A. | $\frac{1}{24}$ | B. | $\frac{1}{19}$ | C. | $\frac{1}{11}$ | D. | $-\frac{23}{8}$ |
分析 由已知中函数$f(x)=\left\{{\begin{array}{l}{{{(\frac{1}{2})}^x}\;x≥4}\\{f(x+1)\;x<4}\end{array}}\right.$,将x=log23代入可得答案.
解答 解:∵函数$f(x)=\left\{{\begin{array}{l}{{{(\frac{1}{2})}^x}\;x≥4}\\{f(x+1)\;x<4}\end{array}}\right.$,
将x=log23∈(1,2)
则f(log23)=f(log23+1)=f(log23+2)=f(log23+3)=$(\frac{1}{2})^{{log}_{2}3+3}$=$\frac{1}{24}$,
故选:A.
点评 本题考查的知识点是分段函数的应用,函数求值,难度不大,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.已知数列{an}为等差数列,a1+a2+a3=3,a5+a6+a7=9,则a10=( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
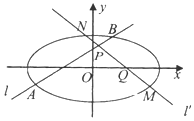 已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$,过$P({0,\frac{b}{2}})$的直线l与椭圆交于A,B两点,过Q(x0,0)(|x0|<a)的直线l'与椭圆交于M,N两点.
已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$,过$P({0,\frac{b}{2}})$的直线l与椭圆交于A,B两点,过Q(x0,0)(|x0|<a)的直线l'与椭圆交于M,N两点.