题目内容
9．若对任意的θ∈R，直线（x-2）cosθ+ysinθ+a=0与圆x2+y2-4x=0相切，则实数a的值是±2．分析 由已知得圆心到直线的距离d=$\frac{|a|}{\sqrt{co{s}^{2}θ+si{n}^{2}θ}}$=2，由此能求出结果．
解答 解：圆x2+y2-4x=0，可化为（x-2）2+y2=4，
∴圆心（2，0）到直线的距离d=$\frac{|a|}{\sqrt{co{s}^{2}θ+si{n}^{2}θ}}$=2，
∴a=±2，
故答案为：±2．
点评 本题考查实数值的求法，是基础题，解题时要认真审题，注意圆的性质和点到直线的距离公式的合理运用．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
17．设F为抛物线C：y2=2px（p＞0）的焦点，曲线y=$\frac{k}{x}$（k＞0）与C交于点A，直线FA恰与曲线y=$\frac{k}{x}$（k＞0）相切于点A，FA交C的准线于点B，则$\frac{|FA|}{|BA|}$等于（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{3}$ | C． | $\frac{2}{3}$ | D． | $\frac{3}{4}$ |
4．椭圆$\frac{{x}^{2}}{5}$+$\frac{{y}^{2}}{4}$=1的左焦点为F，直线x=a与椭圆相交于点M、N，当△FMN的周长最大时，△FMN的面积是（ ）
| A． | $\frac{\sqrt{5}}{5}$ | B． | $\frac{6\sqrt{5}}{5}$ | C． | $\frac{8\sqrt{5}}{5}$ | D． | $\frac{4\sqrt{5}}{5}$ |
1．已知随圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）与过原点的直线交于A、B两点，右焦点为F，∠AFB=120°，若△AFB的面积为4$\sqrt{3}$，则椭圆E的焦距的取值范围是（ ）
| A． | [2，+∞） | B． | [4，+∞） | C． | [2$\sqrt{3}$，+∞） | D． | [4$\sqrt{3}$，+∞） |
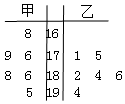在一次水稻试验田验收活动中，将甲、乙两种水稻随机抽取各6株样品，单株籽粒数制成如图所示的茎叶图：