题目内容
1.已知随圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)与过原点的直线交于A、B两点,右焦点为F,∠AFB=120°,若△AFB的面积为4$\sqrt{3}$,则椭圆E的焦距的取值范围是( )| A. | [2,+∞) | B. | [4,+∞) | C. | [2$\sqrt{3}$,+∞) | D. | [4$\sqrt{3}$,+∞) |
分析 利用三角形的面积公式和椭圆的性质得出a≥4,再根据三角形的面积公式得出当A与短轴端点重合时,c取得最小值,利用椭圆的性质求出2c的最小值即可.
解答 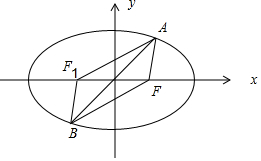 解:取椭圆的左焦点F1,连接AF1,BF1,
解:取椭圆的左焦点F1,连接AF1,BF1,
则AB与FF1互相平分,
∴四边形AFBF1是平行四边形,
∴AF1=BF,
∵AF+AF1=2a,∴AF+BF=2a,
∵S△ABF=$\frac{1}{2}$AF•BF•sin120°=$\frac{\sqrt{3}}{4}$AF•BF=4$\sqrt{3}$,
∴AF•BF=16,
∵2a=AF+BF≥2$\sqrt{AF•BF}$=8,∴a≥4,
又S△ABF=$\frac{1}{2}×c×2|{y}_{A}|$=c•|yA|=4$\sqrt{3}$,
∴c=$\frac{4\sqrt{3}}{|{y}_{A}|}$,
∴当|yA|=b=$\sqrt{{a}^{2}-{c}^{2}}$时,c取得最小值,此时b=$\sqrt{3}$c,
∴a2=3c2+c2=4c2,∴2c=a,
∴2c≥4.
故选B.
点评 本题考查了椭圆的性质,直线与椭圆的位置关系,属于中档题.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
12.已知△ABC中,D为BC边上一点,∠BAD=∠CAD,|$\overrightarrow{AB}$|=3,|$\overrightarrow{AC}$|=2,∠BAC=$\frac{π}{3}$,则$\overrightarrow{AD}•\overrightarrow{BC}$=( )
| A. | $-\frac{8}{5}$ | B. | $\frac{9}{5}$ | C. | $-\frac{9}{5}$ | D. | $\frac{8}{5}$ |
16.已知直线l过椭圆C:$\frac{x^2}{2}+{y^2}=1$的左焦点F且交椭圆C于A、B两点.O为坐标原点,若OA⊥OB,则点O到直线AB的距离为( )
| A. | $\frac{{\sqrt{6}}}{3}$ | B. | 2 | C. | $\frac{{\sqrt{5}}}{2}$ | D. | $\frac{3}{2}$ |
6.某羽绒服卖场为了解气温对营业额的影响,营业员小孙随机记录了该店3月份上旬中某5天的日营业额y(单位:千元)与该地当日最低气温x(单位:℃)的数据,如表:
(1)求y关于x的回归直线方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$;
(2)若天气预报明天的最低气温为12℃,用所求回归方程预测该店明天的营业额;
(3)设该地3月份的日最低气温X~N(μ,σ2),其中μ近似为样本平均数,σ2近似为样本方差,求P(0.6<X<10.2).
附:(1)回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$,$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{x}_{i}^{n}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
22+52+82+92+112=295,2×12+5×10+8×8+9×8+11×7=287.
(2)$\sqrt{10}$=3.2;若X~N(μ,σ2),则P(μ-σ<X<μ+σ)=0.6827.P(μ-2σ<X<μ+2σ)=0.9545.
| x | 2 | 5 | 8 | 9 | 11 |
| y | 12 | 10 | 8 | 8 | 7 |
(2)若天气预报明天的最低气温为12℃,用所求回归方程预测该店明天的营业额;
(3)设该地3月份的日最低气温X~N(μ,σ2),其中μ近似为样本平均数,σ2近似为样本方差,求P(0.6<X<10.2).
附:(1)回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$,$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{x}_{i}^{n}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
22+52+82+92+112=295,2×12+5×10+8×8+9×8+11×7=287.
(2)$\sqrt{10}$=3.2;若X~N(μ,σ2),则P(μ-σ<X<μ+σ)=0.6827.P(μ-2σ<X<μ+2σ)=0.9545.
13.在公差大于0的等差数列{an}中,2a7-a13=1,且a1,a3-1,a6+5成等比数列,则数列{(-1)n-1an}的前21项和为( )
| A. | 21 | B. | -21 | C. | 441 | D. | -441 |