题目内容
4.椭圆$\frac{{x}^{2}}{5}$+$\frac{{y}^{2}}{4}$=1的左焦点为F,直线x=a与椭圆相交于点M、N,当△FMN的周长最大时,△FMN的面积是( )| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{6\sqrt{5}}{5}$ | C. | $\frac{8\sqrt{5}}{5}$ | D. | $\frac{4\sqrt{5}}{5}$ |
分析 设右焦点为F′,连接MF′,NF′,由于|MF′|+|NF′|≥|MN|,可得当直线x=a过右焦点时,△FMN的周长最大.c=$\sqrt{5-4}$=1.把c=1代入椭圆标准方程可得:$\frac{1}{5}+\frac{{y}^{2}}{4}$=1,解得y,即可得出此时△FMN的面积S.
解答 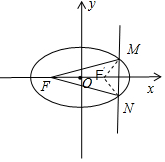 解:设右焦点为F′,连接MF′,NF′,∵|MF′|+|NF′|≥|MN|,
解:设右焦点为F′,连接MF′,NF′,∵|MF′|+|NF′|≥|MN|,
∴当直线x=a过右焦点时,△FMN的周长最大.
由椭圆的定义可得:△FMN的周长的最大值=4a=4$\sqrt{5}$.
c=$\sqrt{5-4}$=1.
把c=1代入椭圆标准方程可得:$\frac{1}{5}+\frac{{y}^{2}}{4}$=1,解得y=±$\frac{4}{\sqrt{5}}$.
∴此时△FMN的面积S=$\frac{1}{2}×2×2×\frac{4}{\sqrt{5}}$=$\frac{8\sqrt{5}}{5}$.
故选:C.
点评 本题考查了椭圆的定义标准方程及其性质、三角形的三边大小关系与三角形面积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.已知△ABC中,D为BC边上一点,∠BAD=∠CAD,|$\overrightarrow{AB}$|=3,|$\overrightarrow{AC}$|=2,∠BAC=$\frac{π}{3}$,则$\overrightarrow{AD}•\overrightarrow{BC}$=( )
| A. | $-\frac{8}{5}$ | B. | $\frac{9}{5}$ | C. | $-\frac{9}{5}$ | D. | $\frac{8}{5}$ |
16.已知直线l过椭圆C:$\frac{x^2}{2}+{y^2}=1$的左焦点F且交椭圆C于A、B两点.O为坐标原点,若OA⊥OB,则点O到直线AB的距离为( )
| A. | $\frac{{\sqrt{6}}}{3}$ | B. | 2 | C. | $\frac{{\sqrt{5}}}{2}$ | D. | $\frac{3}{2}$ |
13.在公差大于0的等差数列{an}中,2a7-a13=1,且a1,a3-1,a6+5成等比数列,则数列{(-1)n-1an}的前21项和为( )
| A. | 21 | B. | -21 | C. | 441 | D. | -441 |