题目内容
16.已知函数f(x)=|x+3|+|2x-4|.(1)当x∈[-3,3]时,解关于x的不等式f(x)<6;
(2)求证:?t∈R,f(x)≥4-2t-t2.
分析 (1)通过讨论a的范围,求出不等式的解集即可;
(2)求出f(x)的分段函数的形式,求出f(x)的最小值,得到关于t的不等式,证出即可.
解答 解:(1)当-3≤x≤2时,f(x)=x+3-(2x-4)=-x+7,
故原不等式可化为-x+7<6,
解得:x>1,故1<x≤2;
当2<x≤3时,f(x)=x+3+(2x-4)=3x-1,
故原不等式可化为3x-1<6,解得$2<x<\frac{7}{3}$;
综上,可得原不等式的解集为$\left\{{x|1<x<\frac{7}{3}}\right\}$.
(2)证明:$f(x)=\left\{{\begin{array}{l}{-3x+1,x≤-3}\\{-x+7,-3<x≤2}\\{3x-1,x>2}\end{array}}\right.$,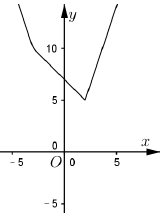
由图象,可知f(x)≥5,
又因为4-2t-t2=-(t+1)2+5≤5,
所以f(x)≥4-2t-t2.
点评 本题考查了解绝对值不等式问题,考查分类讨论思想以及转化思想,是一道中档题.

练习册系列答案
相关题目
6.已知命题p:对任意x∈R,总有2x>x2;q:“ab>4”是“a>2,b>2”的充分不必要条件,则下列命题为真命题的是( )
| A. | p∧q | B. | ¬p∧q | C. | p∧¬q | D. | ¬p∧¬q |
4.在△ABC中,$A=\frac{π}{3},AB=2$,其面积等于$\frac{{\sqrt{3}}}{2}$,则BC等于( )
| A. | $\sqrt{3}$ | B. | $\sqrt{7}$ | C. | 3 | D. | 7 |
12.已知△ABC中,D为BC边上一点,∠BAD=∠CAD,|$\overrightarrow{AB}$|=3,|$\overrightarrow{AC}$|=2,∠BAC=$\frac{π}{3}$,则$\overrightarrow{AD}•\overrightarrow{BC}$=( )
| A. | $-\frac{8}{5}$ | B. | $\frac{9}{5}$ | C. | $-\frac{9}{5}$ | D. | $\frac{8}{5}$ |