题目内容
17．
如图，为测量塔高AB，选取与塔底B在同一水平面内的两点C、D，在C、D两点处测得塔顶A的仰角分别为45°，30°，又测得∠CBD=30°，CD=50米，则塔高AB=（ ）| A． | 50米 | B． | 25$\sqrt{3}$米 | C． | 25米 | D． | 50$\sqrt{3}$米 |
分析 设AB=am，则BC=am，BD=$\sqrt{3}$am，根据∠CBD=30°，CD=50米，利用余弦定理建立方程，即可得出结论．
解答 解：设AB=am，则BC=am，BD=$\sqrt{3}$am，
∵∠CBD=30°，CD=50米，
∴2500=a2+3a2-2a$•\sqrt{3}a•\frac{\sqrt{3}}{2}$，
∴a=50m．
故选A．
点评 本题主要考查了余弦定理的应用，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
8．如果方程Ax+By+C=0表示的直线是x轴，则A、B、C满足（ ）
| A． | A•C=0 | B． | B≠0 | C． | B≠0且A=C=0 | D． | A•C=0且B≠0 |
5．如图，正四面体ABCD的棱长为1，点E是棱CD的中点，则$\overrightarrow{AE}$•$\overrightarrow{AB}$=（ ）
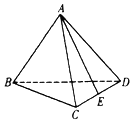
| A． | -$\frac{1}{4}$ | B． | -$\frac{1}{2}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{2}$ |
9．在△ABC中，a=2，$B=\frac{π}{3}$，△ABC的面积等于$\frac{\sqrt{3}}{2}$，则b等于（ ）
| A． | $\frac{\sqrt{3}}{2}$ | B． | 1 | C． | $\sqrt{3}$ | D． | 2 |