题目内容
设动点P(x,y)(x≥0)到定点F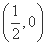 的距离比到y轴的距离大
的距离比到y轴的距离大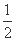 .记点P的轨迹为曲线C.
.记点P的轨迹为曲线C.
(1)求点P的轨迹方程;
(2)设圆M过A(1,0),且圆心M在P的轨迹上,BD是圆M在y轴上截得的弦,当M运动时弦长BD是否为定值?说明理由;
(3)过F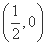 作互相垂直的两直线交曲线C于G、H、R、S,求四边形GRHS面积的最小值.
作互相垂直的两直线交曲线C于G、H、R、S,求四边形GRHS面积的最小值.
解:(1)由题意知,所求动点P(x,y)的轨迹为以F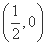 为焦点,直线l:x=-
为焦点,直线l:x=-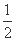 为准线的抛物线,其方程为y2=2x.
为准线的抛物线,其方程为y2=2x.
(2)是定值.解法如下:设圆心M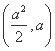 ,
,
半径r=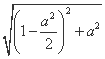 ,
,
圆的方程为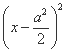 +(y-a)2=a2+
+(y-a)2=a2+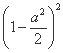 ,
,
令x=0,得B(0,1+a),D(0,-1+a),
∴BD=2,即弦长BD为定值.
(3)设过F的直线GH的方程为y=k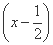 ,G(x1,y1),H(x2,y2),
,G(x1,y1),H(x2,y2),
由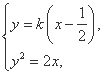 得k2x2-(k2+2)x+
得k2x2-(k2+2)x+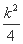 =0,
=0,
∴x1+x2=1+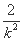 ,x1x2=
,x1x2= ,
,
∴|GH|=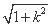 ·
·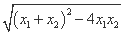 =2+
=2+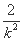 ,
,
同理得|RS|=2+2k2.
S四边形GRHS=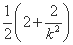 (2+2k2)=2
(2+2k2)=2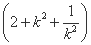 ≥8(当且仅当k=±1时取等号).
≥8(当且仅当k=±1时取等号).
∴四边形GRHS面积的最小值为8.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
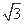 ,且其三个顶点均在抛物线E:x2=2py
,且其三个顶点均在抛物线E:x2=2py
 的垂线,垂足为M,则∠MAF的平分线所在直线的方程为 .
的垂线,垂足为M,则∠MAF的平分线所在直线的方程为 . 

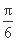 处取得最大值2,其图象与x轴的相邻两个交点的距离为
处取得最大值2,其图象与x轴的相邻两个交点的距离为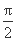 .
.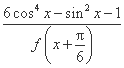 的值域.
的值域.