题目内容
将标号为1,2,3,4,5,6的6个小球放入3个不同的盒子中,若每盒放2个,则标号为1,6的小球不在同一盒中的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:古典概型及其概率计算公式
专题:概率与统计
分析:将标号为1,2,3,4,5,6的6个小球放入3个不同的盒子中,每盒放2个,基本事件总数n=
=90,标号为1,6的小球不在同一盒中,包含的基本事件个数m=
-3C42=90-18=72,由此能求出标号为1,6的小球不在同一盒中的概率.
| C | 2 6 |
| C | 2 4 |
| C | 2 2 |
| C | 2 6 |
| C | 2 4 |
| C | 2 2 |
解答:
解:将标号为1,2,3,4,5,6的6个小球放入3个不同的盒子中,每盒放2个,
基本事件总数n=
=90,
先从3个盒子中选一个放标号为1,6的小球,有3种不同的选法,
再从剩下的4个小球中选两个,放一个盒子有C42=6种放法,
余下放入最后一个盒子,
∴1,6的小球在同一盒中的放法共有3C42=18种,
故标号为1,6的小球不在同一盒中,包含的基本事件个数为:
m=
-3C42=90-18=72,
∴标号为1,6的小球不在同一盒中的概率为:
p=
=
=
.
故选:A.
基本事件总数n=
| C | 2 6 |
| C | 2 4 |
| C | 2 2 |
先从3个盒子中选一个放标号为1,6的小球,有3种不同的选法,
再从剩下的4个小球中选两个,放一个盒子有C42=6种放法,
余下放入最后一个盒子,
∴1,6的小球在同一盒中的放法共有3C42=18种,
故标号为1,6的小球不在同一盒中,包含的基本事件个数为:
m=
| C | 2 6 |
| C | 2 4 |
| C | 2 2 |
∴标号为1,6的小球不在同一盒中的概率为:
p=
| m |
| n |
| 72 |
| 90 |
| 4 |
| 5 |
故选:A.
点评:本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,一个空间几何体的正视图和侧视图都是边长为2的正方形,俯视图是一个圆,那么这个几何体的表面积为( )
如图所示,一个空间几何体的正视图和侧视图都是边长为2的正方形,俯视图是一个圆,那么这个几何体的表面积为( )| A、3π | B、4π | C、5π | D、6π |
在下面四个图中,有一个是函数f(x)=
x3+ax2+(a2-1)x+1(a∈R,a≠0)的导函f′(x)的图象,f(-1)等于( )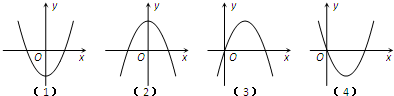
| 1 |
| 3 |
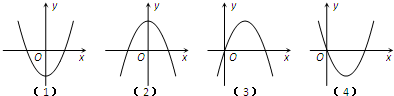
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
函数f(x)=x2-2x+2,若函数f(x+m)是偶函数,那么m的值是( )
| A、1 | B、-1 | C、2 | D、-2 |