题目内容
在下面四个图中,有一个是函数f(x)=
x3+ax2+(a2-1)x+1(a∈R,a≠0)的导函f′(x)的图象,f(-1)等于( )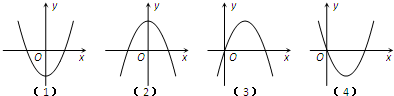
| 1 |
| 3 |
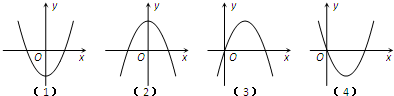
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
考点:导数的加法与减法法则
专题:导数的概念及应用
分析:求函数的导数,确定f′(x)的图象,即可确定a的值.
解答:
解:函数的f(x)的导数f′(x)=x2+2ax+(a2-1)=[x+(a-1)][x+(a+1)],
则f′(x)的图象开口向上,排除(2)(3),
若是(1)则,对称轴关于y轴对称,则2a=0,即a=0,与条件矛盾,排除(1),
则对应的图象应为(4),
则函数过原点,则小根为-a-1=0,解得a=-1,
则f(x)=
x3-x2+(a2-1)x+1,即f(-1)=-
-1+1=-
,
故选:B
则f′(x)的图象开口向上,排除(2)(3),
若是(1)则,对称轴关于y轴对称,则2a=0,即a=0,与条件矛盾,排除(1),
则对应的图象应为(4),
则函数过原点,则小根为-a-1=0,解得a=-1,
则f(x)=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
故选:B
点评:本题主要考查函数图象的确定,以及导数的基本运算.

练习册系列答案
相关题目
为了得到函数y=lg(x+3)-1的图象,只需把函数y=lgx的图象上所有的点( )
| A、向左平移3个单位长度,再向上平移1个单位长度 |
| B、向右平移3个单位长度,再向上平移1个单位长度 |
| C、向左平移3个单位长度,再向下平移1个单位长度 |
| D、向右平移3个单位长度,再向下平移1个单位长度 |
 同时转动如图所示的两个转盘,记转盘甲得到的数为x,转盘乙得到的数为y,构成数对(x,y),则所有数对(x,y)中满足xy=6的概率为( )
同时转动如图所示的两个转盘,记转盘甲得到的数为x,转盘乙得到的数为y,构成数对(x,y),则所有数对(x,y)中满足xy=6的概率为( )A、
| ||
B、
| ||
C、
| ||
D、
|
设m、n是空间两条不同的直线,α、β、γ是三个不同的平面,则下列命题是真命题的是( )
| A、如果α⊥γ,β⊥γ,则α∥β | ||
| B、如果α⊥β,m∥α,则m⊥β | ||
C、如果m∥n,n
| ||
| D、如果m⊥α,n⊥α,则m∥n |
将标号为1,2,3,4,5,6的6个小球放入3个不同的盒子中,若每盒放2个,则标号为1,6的小球不在同一盒中的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
设
=(sinx,1),
=(
,cosx),且
∥
,则锐角x为( )
| a |
| b |
| 1 |
| 2 |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
设f(x)是定义在R上奇函数,且当x<0时,f(x)=2x-3,则f(2)等于( )
| A、-1 | ||
B、
| ||
| C、1 | ||
D、-
|