题目内容
曲线C的极坐标方程为ρsin2θ=cosθ,曲线F 的参数方程为
,以极点为原点,极轴为x正半轴建立直角坐标系,则曲线C与曲线F有 个公共点.
|
考点:简单曲线的极坐标方程,参数方程化成普通方程
专题:坐标系和参数方程
分析:曲线C的极坐标方程为 ρsin2θ=cosθ,变为ρ2sin2θ=ρcosθ,化为y2=x.曲线F 的参数方程为
,化为y=x-2.联立解得即可.
|
解答:
解:曲线C的极坐标方程为 ρsin2θ=cosθ,化为ρ2sin2θ=ρcosθ,∴y2=x.
曲线F 的参数方程为
,化为y=x-2.
联立
,
化为y2-y-2=0,
解得
或
.
因此曲线C与曲线F有2个公共点.
故答案为:2.
曲线F 的参数方程为
|
联立
|
化为y2-y-2=0,
解得
|
|
因此曲线C与曲线F有2个公共点.
故答案为:2.
点评:本题考查了极坐标化为直角坐标方程、参数方程化为普通方程、曲线的交点情况,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设m、n是空间两条不同的直线,α、β、γ是三个不同的平面,则下列命题是真命题的是( )
| A、如果α⊥γ,β⊥γ,则α∥β | ||
| B、如果α⊥β,m∥α,则m⊥β | ||
C、如果m∥n,n
| ||
| D、如果m⊥α,n⊥α,则m∥n |
将标号为1,2,3,4,5,6的6个小球放入3个不同的盒子中,若每盒放2个,则标号为1,6的小球不在同一盒中的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
设
=(sinx,1),
=(
,cosx),且
∥
,则锐角x为( )
| a |
| b |
| 1 |
| 2 |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
若命题:对于任意x∈[-1,1],使f(x)≥0的否定是( )
| A、对于任意x∈[-1,1]有f(x)<0 |
| B、对于任意x∈(-∞,-1)∪(1,∞)有f(x)<0 |
| C、存在x0∈[-1,1]使f(x0)<0 |
| D、存在x0∈[-1,1]使f(x0)≥0 |
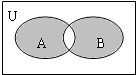 设全集U={x|x<9,且x∈Z},A={1,2,3},B={3,4,5,6},图中阴影部分所表示的集合为( )
设全集U={x|x<9,且x∈Z},A={1,2,3},B={3,4,5,6},图中阴影部分所表示的集合为( )| A、{1,2,3,4,5,6,7,8} |
| B、{1,2,4,5,6} |
| C、{1,2,4,5,6,7,8} |
| D、{1,2,3,4,5,6} |