题目内容
下列函数中,在区间(0,2)上单调递减的是( )
A、y=-
| |||
| B、y=lnx | |||
C、y=-
| |||
| D、y=|x| |
考点:函数单调性的判断与证明
专题:函数的性质及应用
分析:由基本初等函数的单调性定义,判定各选项中的函数是否满足条件即可.
解答:
解:A中,y=-
在(-∞,0)和(0,+∞)上是增函数,∴不满足条件;
B中,y=lnx在定义域(0,+∞)上是增函数,∴不满足条件;
C中,y=-
是定义域上的偶函数,在(0,+∞)上是减函数,∴在(0,2)上是减函数,满足条件;
D中,y=|x|是定义域上的偶函数,在(0,+∞)上是增函数,∴不满足条件;
故选:C.
| 1 |
| x |
B中,y=lnx在定义域(0,+∞)上是增函数,∴不满足条件;
C中,y=-
| 3 | x2 |
D中,y=|x|是定义域上的偶函数,在(0,+∞)上是增函数,∴不满足条件;
故选:C.
点评:本题考查了基本初等函数的单调性问题,是基础题.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
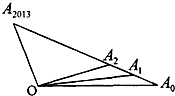 如图,O为线段A0A2013外一点,若A0,A1,A2,A3,…,A2013中任意相邻两点的距离相等,
如图,O为线段A0A2013外一点,若A0,A1,A2,A3,…,A2013中任意相邻两点的距离相等,| OA0 |
| a |
| OA2013 |
| b |
| a |
| b |
| OA0 |
| OA1 |
| OA2 |
| OA2013 |
A、1006(
| ||||
B、1007(
| ||||
C、2012(
| ||||
D、2014(
|
函数f(x)=
x5-x4-4x3+7的极值点的个数是( )
| 1 |
| 5 |
| A、1个 | B、2个 | C、3个 | D、4个 |
已知曲线C:x2+y2-2x+2y=0与直线L:y+2=k(x-2),则C与L的公共点( )
| A、有2个 | B、最多1个 |
| C、至少1个 | D、不存在 |
圆柱的一个底面积为S,侧面展开图是一个正方形,那么这个圆柱的体积是( )
A、
| ||||
B、
| ||||
C、2S
| ||||
D、S
|
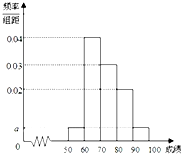 某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].
某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100]. 已知
已知 如图正方形ABCD的边长为4,E、F分别为DC、BC中点.
如图正方形ABCD的边长为4,E、F分别为DC、BC中点.