题目内容
12.已知函数f(x)=x3-ax2+10.(1)当a=1时,求曲线y=f(x)在点(2,f(2))处的切线方程;
(2)在区间[1,2]内存在实数x,使得f(x)<0成立,求实数a的取值范围.
分析 (1)当a=1时,求导数,可得切线斜率,即可求曲线y=f(x)在点(2,f(2))处的切线方程;
(2)由已知得$a>\frac{{{x^3}+10}}{x^2}=x+\frac{10}{x^2}$,求出右边的最小值,即可求实数a的取值范围.
解答 解:(1)当a=1时,f(x)=3x2-2x,f(2)=14,
曲线y=f(x)在点(2,f(2))处的切线斜率k=f'(2)=8,
所以曲线y=f(x)在点(2,f(2))处的切线方程为y-14=8(x-2),即8x-y-2=0.
(2)由已知得$a>\frac{{{x^3}+10}}{x^2}=x+\frac{10}{x^2}$,设$g(x)=x+\frac{10}{x^2}$(1≤x≤2),$g'(x)=1-\frac{20}{x^3}$,
∵1≤x≤2,∴g'(x)<0,∴g(x)在[1,2]上是减函数,$g{(x)_{min}}=g(2)=\frac{9}{2}$,
∴$a>\frac{9}{2}$,即实数a的取值范围是$(\frac{9}{2},+∞)$.
点评 本题考查导数的几何意义,考查函数的单调性与最值,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.对具有线性相关关系的变量x,y,测得一组数据如下
根据表,利用最小二乘法得到它的回归直线方程为( )
| x | 1 | 2 | 3 | 4 |
| y | 4.5 | 4 | 3 | 2.5 |
| A. | y=-0.7x+5.20 | B. | y=-0.7x+4.25 | C. | y=-0.7x+6.25 | D. | y=-0.7x+5.25 |
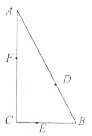 如图,某公园有三条观光大道AB,BC,AC围成直角三角形,其中直角边BC=200m,斜边AB=400m,现有甲、乙、丙三位小朋友分别在AB,BC,AC大道上嬉戏,所在位置分别记为点D,E,F.
如图,某公园有三条观光大道AB,BC,AC围成直角三角形,其中直角边BC=200m,斜边AB=400m,现有甲、乙、丙三位小朋友分别在AB,BC,AC大道上嬉戏,所在位置分别记为点D,E,F.