题目内容

20．函数f（x）=x2-2x+2在（-∞，1）上的反函数f-1（x）=1-$\sqrt{x-1}$．x＞1．

分析 先求出x=1-$\sqrt{y-1}$，y∈（1，+∞），x，y互换，得：反函数f-1（x）．

解答 解：∵函数f（x）=y=x2-2x+2，x∈（-∞，1），
∴x=1-$\sqrt{y-1}$，y∈（1，+∞），
x，y互换，得：反函数f-1（x）=1-$\sqrt{x-1}$．x＞1．
故答案为：1-$\sqrt{x-1}$．x＞1．

点评 本题考查反函数的求法，是基础题，解题时要认真审题，注意反函数性质的合理运用．

练习册系列答案
相关题目
10．已知$\overrightarrow m=（\sqrt{3}，2sinx），\overrightarrow n=（{sin^2}x-{cos^2}x，cosx）$，函数$f（x）=\overrightarrow m•\overrightarrow n$．
（1）求f（x）的最小正周期、对称轴和对称中心；
（2）设$x∈[-\frac{π}{3}，\;\frac{π}{3}]$，求f（x）的单调递增区间．
11．函数f（x）=ax-1+4的图象恒过定点P，则P点坐标是（1，5）．
8．若不等式|x-m|＜1成立的充分不必要条件是1＜x＜2，则实数m的取值范围是[1，2]．
15．设实数a满足log2a=4．则loga2=$\frac{1}{4}$．
5．若a＞b＞c，a+b+c=0，则下列各是正确的是（　　）
A．ab＞acB．ac＞bcC．a|b|＞|b|cD．ab＞bc
12．已知函数f（x）=x3-ax2+10．
（1）当a=1时，求曲线y=f（x）在点（2，f（2））处的切线方程；
（2）在区间[1，2]内存在实数x，使得f（x）＜0成立，求实数a的取值范围．
9．在考试测评中，常用难度曲线图来检测题目的质量，一般来说，全卷得分高的学生，在某道题目上的答对率也应较高，如果是某次数学测试压轴题的第1、2问得分难度曲线图，第1、2问满分均为6分，图中横坐标为分数段，纵坐标为该分数段的全体考生在第1、2问的平均难度，则下列说法正确的是（　　）
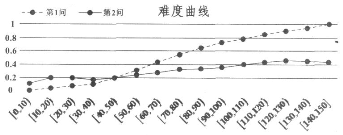
A．此题没有考生得12分
B．此题第1问比第2问更能区分学生数学成绩的好与坏
C．分数在[40，50）的考生此大题的平均得分大约为4.8分
D．全体考生第1问的得分标准差小于第2问的得分标准差
10．已知△ABC的面积为$\sqrt{3}$，且∠C=30°，BC=2$\sqrt{3}$，则AB等于（　　）
A．1B．$\sqrt{3}$C．2D．2$\sqrt{3}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网