题目内容
4.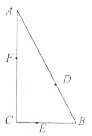 如图,某公园有三条观光大道AB,BC,AC围成直角三角形,其中直角边BC=200m,斜边AB=400m,现有甲、乙、丙三位小朋友分别在AB,BC,AC大道上嬉戏,所在位置分别记为点D,E,F.
如图,某公园有三条观光大道AB,BC,AC围成直角三角形,其中直角边BC=200m,斜边AB=400m,现有甲、乙、丙三位小朋友分别在AB,BC,AC大道上嬉戏,所在位置分别记为点D,E,F.(1)若甲、乙都以每分钟100m的速度从点B出发在各自的大道上奔走,到大道的另一端时即停,乙比甲迟2分钟出发,当乙出发1分钟后,求此时甲乙两人之间的距离;
(2)设∠CEF=θ,乙丙之间的距离是甲乙之间距离的2倍,且∠DEF=$\frac{π}{3}$,请将甲乙之间的距离y表示为θ的函数,并求甲乙之间的最小距离.
分析 (1)由题意,BD=300,BE=100,△BDE中,由余弦定理可得甲乙两人之间的距离;
(2)△BDE中,由正弦定理可得$\frac{200-2ysinθ}{sinθ}$=$\frac{y}{sin60°}$,可将甲乙之间的距离y表示为θ的函数,并求甲乙之间的最小距离.
解答 解:(1)由题意,BD=300,BE=100,
△ABC中,cosB=$\frac{1}{2}$,B=$\frac{π}{3}$,
△BDE中,由余弦定理可得DE=$\sqrt{30{0}^{2}+10{0}^{2}-2•300•100•\frac{1}{2}}$=100$\sqrt{7}$m;
(2)由题意,EF=2DE=2y,∠BDE=∠CEF=θ.
△CEF中,CE=EFcos∠CEF=2ycosθ
△BDE中,由正弦定理可得$\frac{200-2ycosθ}{sinθ}$=$\frac{y}{sin60°}$,
∴y=$\frac{100\sqrt{3}}{sinθ+\sqrt{3}cosθ}$=$\frac{50\sqrt{3}}{sin(θ+\frac{π}{3})}$,0$<θ<\frac{π}{2}$,
∴θ=$\frac{π}{6}$,ymin=50$\sqrt{3}$m.
点评 本题考查利用数学知识解决实际问题,考查正弦、余弦定理的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
9.在考试测评中,常用难度曲线图来检测题目的质量,一般来说,全卷得分高的学生,在某道题目上的答对率也应较高,如果是某次数学测试压轴题的第1、2问得分难度曲线图,第1、2问满分均为6分,图中横坐标为分数段,纵坐标为该分数段的全体考生在第1、2问的平均难度,则下列说法正确的是( )
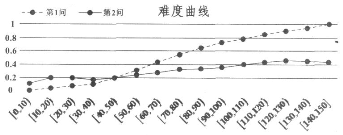

| A. | 此题没有考生得12分 | |
| B. | 此题第1问比第2问更能区分学生数学成绩的好与坏 | |
| C. | 分数在[40,50)的考生此大题的平均得分大约为4.8分 | |
| D. | 全体考生第1问的得分标准差小于第2问的得分标准差 |
14.在△ABC中,a=2,c=1,∠B=60°,那么b等于( )
| A. | $\sqrt{5}$ | B. | $\sqrt{3}$ | C. | 1 | D. | $\frac{{\sqrt{3}}}{2}$ |