题目内容
已知圆C的方程为x2+y2-6x-8y=0.若等差数列{an}中的a1,a2,…,a11是该圆过点(3,8)的11条弦的长,则{an}的公差的最大值是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:数列的求和
专题:等差数列与等比数列
分析:由题意求出圆的直径,并求出过点P(3,5)与直径垂直的弦长,然后由等差数列的通项公式求公差.
解答:
解:∵32+82-6×3-8×8=-15<0,
∴点(3,8)在圆内部,过圆内一点最长的弦是直径,过该点与直径垂直的弦最短,
化x2+y2-6x-8y=0为圆的标准式:(x-3)2+(y-4)2=52,
因此,过(3,8)的弦中,最长为10,最短为2
=6,
故公差最大为d=
=
=
.
故选:B.
∴点(3,8)在圆内部,过圆内一点最长的弦是直径,过该点与直径垂直的弦最短,
化x2+y2-6x-8y=0为圆的标准式:(x-3)2+(y-4)2=52,
因此,过(3,8)的弦中,最长为10,最短为2
| 52-42 |
故公差最大为d=
| a11-a1 |
| 10 |
| 10-6 |
| 10 |
| 2 |
| 5 |
故选:B.
点评:本题考查了等差数列的通项公式,考查了直线与圆的位置关系,关键是对题意的理解,是中档题.

练习册系列答案
相关题目
点A(2,0),B(4,2),若|
|=2|
|,则点C坐标为( )
| AB |
| AC |
| A、(1,-1) |
| B、(1,-1)或(5,-1) |
| C、(1,-1)或(3,1) |
| D、无数多个 |
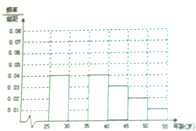 某班同学利用五一劳动节进行社会实践,对信宜城区[25,55]岁的人群随机抽取n人进行生活习惯是否符合低碳观念的调查.得到如图所示的人数频率分布直方图,若生活习惯符合低碳观念,则称为“低碳族”,否则称为“非低碳族”,得到如图所示的人数统计表.
某班同学利用五一劳动节进行社会实践,对信宜城区[25,55]岁的人群随机抽取n人进行生活习惯是否符合低碳观念的调查.得到如图所示的人数频率分布直方图,若生活习惯符合低碳观念,则称为“低碳族”,否则称为“非低碳族”,得到如图所示的人数统计表.