题目内容

如图，E为正方体的棱AA1的中点，F为棱AB上的一点，且∠C1EF=90°，则AF：FB=（　　）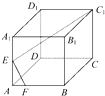
A、1：1B、1：2
C、1：3D、1：4
考点：棱柱的结构特征
专题：空间位置关系与距离
分析：设出正方体的棱长，求出C1E，利用∠C1EF=90°，通过C1F求出x的值，即可得到结果．
解答： 解：解：设正方体的棱长为：2，由题意可知C1E=
12+(2
2
)2
=3，
∠C1EF=90°，所以设AF=x，12+x2+C1E2=22+22+（2-x）2，
解得：x=
1
2
，所以AF：FB=
1
2
：
1
3
=1：3；
故选：C．
点评：本题是基础题，考查正方体的变的计算，考查直角三角形的利用，长方体的性质，考查计算能力．
练习册系列答案
相关题目
已知f（x）=3x2-4x+5，g（x）=f（x-2），则g（3）=
 
．
不等式log
1
3
（-x）＞-x-1的解集为
 
．
已知点P（x，y）为圆C：x2+y2-4x+3=0上一点，C为圆心．
（1）求x2+y2的取值范围；
（2）求
y
x
的最大值；
（3）求
PC
•
PO
（O为坐标原点）的取值范围．
已知点M（1，m），圆C：x2+y2=4．
（1）若过点M的圆C的切线只有一条，求m的值及切线方程；
（2）若过点M且在两坐标轴上的截距相等的直线被圆C截得的弦长为2
3
，求m的值．
过原点O的圆C，与x轴相交于点A（4，0），与y轴相交于点B（0，2）．
（1）求圆C的标准方程；
（2）直线l过B点与圆C相切，求直线L的方程，并化为一般式．
∫
2
1
(
1
x
+
1
x2
+
1
x3
)dx=（　　）
A、ln 2+
7
8
B、ln 2-
7
2
C、ln 2-
5
8
D、ln 2-
17
8
计算：2log32-2log3
32
9
．
若函数f（x）是定义域D内的某个区间I上的增函数，且F（x）=
f(x)
x
在I上是减函数，则称y=f（x）是I上的“非完美增函数”，已知f（x）=lnx，g（x）=2x+
2
x
+alnx（a∈R）
（1）判断f（x）在（0，1]上是否是“非完美增函数”；
（2）若g（x）是[1，+∞）上的“非完美增函数”，求实数a的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网