题目内容
函数f（x）=x3+x-3的零点落在的区间是（ ）
| A、[0，1] |
| B、[1，2] |
| C、[2，3] |
| D、[3，4] |
考点：函数零点的判定定理
专题：函数的性质及应用
分析：把区间端点函数值代入验证即可．
解答：
解：∵f（x）=x3+x-3单调递增，
∴f（0）=-3＜0
f（1）=1+1-3=-1＜0
f（2）=8+2-3=7＞0
∴f（x）=x3+x-3在区间（1，2）有一个零点，
故选：B．
∴f（0）=-3＜0
f（1）=1+1-3=-1＜0
f（2）=8+2-3=7＞0
∴f（x）=x3+x-3在区间（1，2）有一个零点，
故选：B．
点评：考查方程的根和函数零点之间的关系，即函数零点的判定定理，体现了转化的思想方法，属基础题．
练习册系列答案
启东小题作业本系列答案
相关题目
已知A是三角形的一内角，且sinA+cosA=
，则cos2A=（ ）
| 1 |
| 3 |
A、
| ||||
B、-
| ||||
C、±
| ||||
D、-
|
关于x的不等式x2+x+c＞0的解集是全体实数的条件是（ ）
A、c＜
| ||
B、c≤
| ||
C、c＞
| ||
D、c≥
|
某小朋友用手指按如图所示的规则练习数数，数到2009时对应的指头是（ ）
| A、大拇指 | B、食指 |
| C、中指 | D、无名指 |
若3sinx-
cosx=2
sin（x-φ），φ∈（-π，π），则φ=（ ）
| 3 |
| 3 |
A、-
| ||
B、
| ||
C、
| ||
D、-
|
在极坐标系中，圆ρ=4cosθ的垂直于极轴的两条切线方程分别为（ ）
| A、θ=0（ρ∈R）和ρcosθ=4 | ||
B、θ=
| ||
| C、θ=0（ρ∈R）和ρcosθ=2 | ||
D、θ=
|
（x-1）5的展开式中，x3的系数为 （ ）
| A、-10 | B、-5 | C、5 | D、10 |
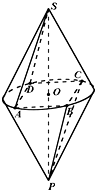如图两个共底面的相同的圆锥，底面圆心为O，顶点分别为S和P，四边形ABCD是圆O的内接矩形，连接SA，SD，PC，PB