题目内容
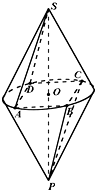 如图两个共底面的相同的圆锥,底面圆心为O,顶点分别为S和P,四边形ABCD是圆O的内接矩形,连接SA,SD,PC,PB
如图两个共底面的相同的圆锥,底面圆心为O,顶点分别为S和P,四边形ABCD是圆O的内接矩形,连接SA,SD,PC,PB(1)证明平面SAD∥平面PBC
(2)圆O的圆周上是否存在点M使平面SOM⊥平面SAD,若存在写出存在的理由,并给予证明,若不存在说明理由.
(3)若SA=2,AB=BC=2,求三棱锥S-PBC的体积.
考点:棱柱、棱锥、棱台的体积,平面与平面平行的判定
专题:综合题,空间位置关系与距离
分析:(1)连接BD,SB,PD,证明四边形SDPB是菱形,可得PB∥平面SDA,证明BC∥平面SDA,即可证明平面SAD∥平面PBC;
(2)过点O作直线AD的垂线交圆于两个点都可以作为存在点M,即可证明平面SOM⊥平面SAD;
(3)利用VS-PBC=
S△SPB•CO,即可求三棱锥S-PBC的体积.
(2)过点O作直线AD的垂线交圆于两个点都可以作为存在点M,即可证明平面SOM⊥平面SAD;
(3)利用VS-PBC=
| 1 |
| 3 |
解答:
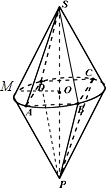 证明:(1)连接BD,SB,PD,则
证明:(1)连接BD,SB,PD,则
∵四边形ABCD是圆O的内接矩形,
∴BD过圆心O,
∴S,D,P,B四点共面,
∵两个共底面的相同的圆锥,
∴SD=DP=PB-BS,
∴四边形SDPB是菱形,
∴PB∥SD,
∴PB∥平面SDA,
∵BC∥AD,
∴BC∥平面SDA,
∵PB∥平面SDA,BC∥平面SDA,PB∩BC=B,
∴平面SAD∥平面PBC
(2)解:过点O作直线AD的垂线交圆于两个点都可以作为存在点M.
∵SO⊥圆O,
∴AD⊥SO,
∵AD⊥SO,AD⊥OM,OM∩SO=O,
∴AD⊥平面SOM,
∴平面SOM⊥平面SAD;
(3)解:∵AB=BC=2,
∴四边形ABCD是圆O的边长为2的内接正方形,
∴VS-PBC=
S△SPB•CO=
.
 证明:(1)连接BD,SB,PD,则
证明:(1)连接BD,SB,PD,则∵四边形ABCD是圆O的内接矩形,
∴BD过圆心O,
∴S,D,P,B四点共面,
∵两个共底面的相同的圆锥,
∴SD=DP=PB-BS,
∴四边形SDPB是菱形,
∴PB∥SD,
∴PB∥平面SDA,
∵BC∥AD,
∴BC∥平面SDA,
∵PB∥平面SDA,BC∥平面SDA,PB∩BC=B,
∴平面SAD∥平面PBC
(2)解:过点O作直线AD的垂线交圆于两个点都可以作为存在点M.
∵SO⊥圆O,
∴AD⊥SO,
∵AD⊥SO,AD⊥OM,OM∩SO=O,
∴AD⊥平面SOM,
∴平面SOM⊥平面SAD;
(3)解:∵AB=BC=2,
∴四边形ABCD是圆O的边长为2的内接正方形,
∴VS-PBC=
| 1 |
| 3 |
2
| ||
| 3 |
点评:本题考查平面与平面平行、垂直,考查三棱锥体积的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
函数f(x)=x3+x-3的零点落在的区间是( )
| A、[0,1] |
| B、[1,2] |
| C、[2,3] |
| D、[3,4] |
 如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.
如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.