题目内容
解关于x的不等式：x（6-x）≥-16．
考点：一元二次不等式的解法
专题：不等式的解法及应用
分析：变形不等式，分解因式可得（x-8）（x+2）≤0，易得解集．
解答：
解：原不等式可化为6x-x2≥-16，
整理可得x2-6x-16≤0，
分解因式可得（x-8）（x+2）≤0，
解得-2≤x≤8，
∴原不等式的解集为：{x|-2≤x≤8}
整理可得x2-6x-16≤0，
分解因式可得（x-8）（x+2）≤0，
解得-2≤x≤8，
∴原不等式的解集为：{x|-2≤x≤8}
点评：本题考查一元二次不等式的解法，属基础题．
练习册系列答案
中考解读考点精练系列答案
相关题目
函数y=
x2-lnx的单调减区间是（ ）注：（lnx）′=
．
| 1 |
| 2 |
| 1 |
| x |
| A、（-∞，-1） |
| B、（0，1）∪（-∞，-1） |
| C、（0，1） |
| D、（-∞，+∞） |
函数f（x）=x3+x-3的零点落在的区间是（ ）
| A、[0，1] |
| B、[1，2] |
| C、[2，3] |
| D、[3，4] |
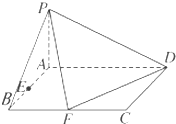已知四棱锥P-ABCD底面ABCD是矩形PA⊥平面ABCD，AD=2，AB=1，E、F分别是线段AB，BC的中点，