题目内容
若3sinx-
cosx=2
sin(x-φ),φ∈(-π,π),则φ=( )
| 3 |
| 3 |
A、-
| ||
B、
| ||
C、
| ||
D、-
|
考点:两角和与差的正弦函数
专题:三角函数的求值
分析:先利用两角和公式对等号左边进行化简进而根据φ的范围求得φ.
解答:
解:3sinx-
cosx=2
(
sinx-
cosx)=2
sin(x-
)=2
sin(x-φ),
∴φ=2kπ+
,k∈Z,
∵φ∈(-π,π),
∴φ=
,
故选:B.
| 3 |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| π |
| 6 |
| 3 |
∴φ=2kπ+
| π |
| 6 |
∵φ∈(-π,π),
∴φ=
| π |
| 6 |
故选:B.
点评:本题主要考查了两角和与差的正弦函数公式的应用,诱导公式的应用.对三角函数的基础公式应能够熟练记忆和灵活运用.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
若命题“¬(p∨q)”为真命题,则( )
| A、p,q均为假命题 |
| B、p,q中至多有一个为真命题 |
| C、p,q均为真命题 |
| D、p,q中至少有一个为真命题 |
若(a+2i)i=b+i,其中a,b∈R,i是虚数单位,则a-b=( )
| A、-3 | B、-2 | C、2 | D、3 |
函数f(x)=x3+x-3的零点落在的区间是( )
| A、[0,1] |
| B、[1,2] |
| C、[2,3] |
| D、[3,4] |
线性回归方程表示的直线
=bx+a必经过( )
 |
| y |
| A、(0,0) | ||||
B、(
| ||||
C、(
| ||||
D、(0,
|

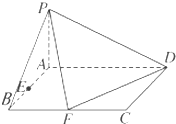 已知四棱锥P-ABCD底面ABCD是矩形PA⊥平面ABCD,AD=2,AB=1,E、F分别是线段AB,BC的中点,
已知四棱锥P-ABCD底面ABCD是矩形PA⊥平面ABCD,AD=2,AB=1,E、F分别是线段AB,BC的中点,