题目内容
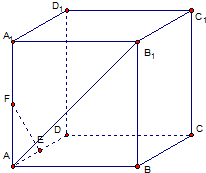 如图,在正方体ABCD-A1B1C1D1中,E、F分别是AD,AA1的中点
如图,在正方体ABCD-A1B1C1D1中,E、F分别是AD,AA1的中点(1)求直线AB1和直线CC1所成的角的大小
(2)求直线AB1和直线EF所成的角的大小.
考点:异面直线及其所成的角
专题:空间角
分析:通过建立空间直角坐标系,利用向量的夹角公式即可得出异面直线所成的夹角.
解答:
解:如图所示,建立空间直角坐标系.
(1)不妨设正方形的棱长为2.则A(2,0,0),B1(2,2,2),C(0,2,0),C1(0,2,2).
则
=(0,2,2),
=(0,0,2).
∴cos<
,
>=
=
=
,
∴直线AB1和直线CC1所成的角的大小为45°.
(2)E(1,0,0),F(2,0,1).
∴
=(1,0,1).
∴cos<
,
>=
=
=
.
∴直线AB1和直线EF所成的角的大小为60°.

(1)不妨设正方形的棱长为2.则A(2,0,0),B1(2,2,2),C(0,2,0),C1(0,2,2).
则
| AB1 |
| CC1 |
∴cos<
| AB1 |
| CC1 |
| ||||
|
|
| 4 | ||
|
| ||
| 2 |
∴直线AB1和直线CC1所成的角的大小为45°.
(2)E(1,0,0),F(2,0,1).
∴
| EF |
∴cos<
| AB1 |
| EF |
| ||||
|
|
| 2 | ||||
|
| 1 |
| 2 |
∴直线AB1和直线EF所成的角的大小为60°.
点评:本题考查了利用向量的夹角公式得出异面直线所成的夹角,考查了间想象能力,考查了推理能力和计算能力,属于基础题.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
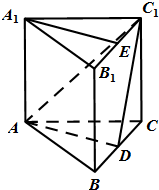 如图,正三棱柱ABC-A1B1C1的侧棱为2,底面是边长为2的等边三角形,D,E分别是线段BC,B1C1的中点.
如图,正三棱柱ABC-A1B1C1的侧棱为2,底面是边长为2的等边三角形,D,E分别是线段BC,B1C1的中点.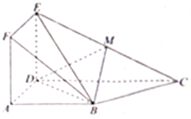 如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AD=
如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AD=