Question

设函数f（x）=

x2+bx+c (x≤0) 2 (x＞0)

，若f（-2）=f（0），f（-1）=-3，则关于x的方程f（x）=x的解的个数为

 

．

Answer 1

考点：根的存在性及根的个数判断

专题：函数的性质及应用

分析：由题意求得b、c的值，可得函数f（x）的解析式．关于x的方程f（x）=x的解的个数即函数f（x）的图象和直线y=x的交点个数，数形结合可得结论．

解答： 解：∵函数f（x）=

x2+bx+c (x≤0) 2 (x＞0)

 满足f（-2）=f（0），可得-

b

2

=-1，∴b=2．
再根据 f（-1）=-3，可得1-2+c=-3，∴c=-2，
∴f（x）=

x2+2x-2 ， x≤0 2  ，x＞0

．
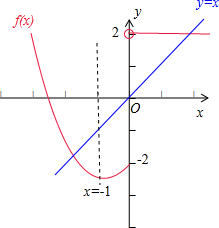
关于x的方程f（x）=x的解的个数即函数f（x）的图象和直线y=x的交点个数，
数形结合可得函数f（x）的图象和直线y=x的交点个数为2，
故答案为：2．

点评：本题主要考查函数零点个数的判断方法，体现了化归与转化、数形结合的数学思想，属于基础题．