题目内容
若log4（3a+4b）=log2
，则a+b的最小值是 ．
| ab |
考点：基本不等式
专题：不等式的解法及应用
分析：log4（3a+4b）=log2
，可得3a+4b=ab，a，b＞0.b=
＞0，解得a＞4．于是a+b=a+
=a-4+
+7，再利用基本不等式的性质即可得出．
| ab |
| 3a |
| a-4 |
| 3a |
| a-4 |
| 12 |
| a-4 |
解答：
解：∵log4（3a+4b）=log2
，
∴log2
=log2
，
∴
=
，
∴3a+4b=ab，a，b＞0．
∴b=
＞0，解得a＞4．
a+b=a+
=a-4+
+7≥7+2
=7+4
，当且仅当a=4+2
时取等号．
∴a+b的最小值是7+4
．
故答案为：7+4
．
| ab |
∴log2
| 3a+4b |
| ab |
∴
| 3a+4b |
| ab |
∴3a+4b=ab，a，b＞0．
∴b=
| 3a |
| a-4 |
a+b=a+
| 3a |
| a-4 |
| 12 |
| a-4 |
(a-4)•
|
| 3 |
| 3 |
∴a+b的最小值是7+4
| 3 |
故答案为：7+4
| 3 |
点评：本题考查了对数的运算性质、基本不等式的性质，考查了计算能力，属于基础题．
练习册系列答案
开心口算题卡系列答案
口算题卡河北少年儿童出版社系列答案
A加金题 系列答案
相关题目
如图，在长方体ABCD-A1B1C1D1中，已知E、F分别是AB、BC的中点，求证：EF∥A1C1．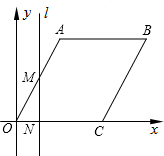
如图，在平面直角坐标系中，四边形OABC是菱形，点C的坐标为（4，0），∠AOC=60°，垂直于x轴的直线l从y轴出发，沿x轴正方向以每秒1个单位长度的速度向右平移，设直线l与菱形OABC的两边分别交于点M，N（点M在点N的上方），若△OMN的面积为S，直线l的运动时间为t秒（0≤t≤4），请求出S与t的函数关系．