题目内容
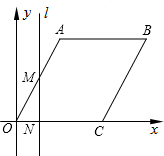 如图,在平面直角坐标系中,四边形OABC是菱形,点C的坐标为(4,0),∠AOC=60°,垂直于x轴的直线l从y轴出发,沿x轴正方向以每秒1个单位长度的速度向右平移,设直线l与菱形OABC的两边分别交于点M,N(点M在点N的上方),若△OMN的面积为S,直线l的运动时间为t秒(0≤t≤4),请求出S与t的函数关系.
如图,在平面直角坐标系中,四边形OABC是菱形,点C的坐标为(4,0),∠AOC=60°,垂直于x轴的直线l从y轴出发,沿x轴正方向以每秒1个单位长度的速度向右平移,设直线l与菱形OABC的两边分别交于点M,N(点M在点N的上方),若△OMN的面积为S,直线l的运动时间为t秒(0≤t≤4),请求出S与t的函数关系.考点:基本不等式在最值问题中的应用
专题:函数的性质及应用
分析:沿x轴正方向运动与菱形OABC的两边相交有2种情况:分别列出0≤t≤2时和当2<t≤4时的函数解析式,进而利用函数的性质确定面积的最大值.
解答:
解:
直线l从y轴出发,沿x轴正方向运动与菱形OABC的两边相交有2种情况:
①0≤t≤2时,直线l与OA、OC两边相交
∵MN⊥OC,
∴ON=t
∴MN=ONtan60°=
t
∴S=
ON•MN=
t2.
②当2<t≤4时,直线l与AB、OC两边相交
S=
ON•MN=
×t×2
=
t.
当0≤t≤2时,Smax=
×22=2
当2<t≤4时,Smax=4
综上所述,当t=4秒时,S的最大值为4
.
直线l从y轴出发,沿x轴正方向运动与菱形OABC的两边相交有2种情况:
①0≤t≤2时,直线l与OA、OC两边相交
∵MN⊥OC,
∴ON=t
∴MN=ONtan60°=
| 3 |
∴S=
| 1 |
| 2 |
| ||
| 2 |
②当2<t≤4时,直线l与AB、OC两边相交
S=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
当0≤t≤2时,Smax=
| ||
| 2 |
| 3 |
当2<t≤4时,Smax=4
| 3 |
综上所述,当t=4秒时,S的最大值为4
| 3 |
点评:本题主要考查了函数在解决实际问题中的应用.解题的关键是建立合适的数学模型.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
函数f(x)的图象由函数g(x)=4sinxcosx的图象向左平移
个单位得到,则f(
)=( )
| π |
| 3 |
| π |
| 4 |
| A、-1 | ||
| B、1 | ||
C、-
| ||
D、
|
已知F1(-3,0),F2(3,0),动点P满足:|PF1|+|PF2|=6,则动点P的轨迹为( )
| A、椭圆 | B、抛物线 |
| C、线段 | D、双曲线 |
若A,B,C分别为△ABC的三个内角,且sinA:sinB:sinC=3:5:7,则△ABC的最大内角是( )
| A、135° | B、90° |
| C、120° | D、150° |
已知函数y=loga(x+b)(a>0且a≠1)的图象如图,则( )
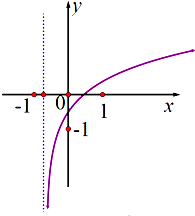

| A、0<a-1<b<1<a |
| B、0<b<a<1<a-1 |
| C、0<a<b<1<a-1 |
| D、0<a<1<a-1<b |
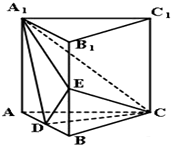 如图:直三棱柱ABC-A1B1C1中,AC=BC=AA1=2,∠ACB=90°.E为的中点,D点在AB上且DE=
如图:直三棱柱ABC-A1B1C1中,AC=BC=AA1=2,∠ACB=90°.E为的中点,D点在AB上且DE=