Question

已知函数f（x）=

1

3

x³-bx²+cx+d，设曲线y=f（x）过点（3，0），且在点（3，0）处的切线的斜率等于4，y=f′（x）为f（x）的导函数，满足f′（2-x）=f′（x）．
（1）求f（x）；
（2）设g（x）=x

f′(x)

，m＞0，求函数g（x）在[0，m]上的最大值；
（3）设h（x）=f′（x）+（2x+1）t，若h（x）＜4对t∈[0，1]恒成立，求实数x的取值范围．

Answer 1

考点：利用导数求闭区间上函数的最值,利用导数研究曲线上某点切线方程

专题：综合题,导数的综合应用

分析：（1）求导数，f′（2-x）=f′（x），可得f′（x）的图象关于直线x=1对称，求出b，再利用f（3）=0，f′（3）=4，求出c，d，即可求f（x）；
（2）g（x）=x

f′(x)

=x|x-1|=

x2-x，x≥1 x-x2，x＜1

，作出函数的图象，即可求函数g（x）在[0，m]上的最大值；
（3）h（x）=f′（x）+（2x+1）t=（x-1）²+（2x+1）t，当t∈[0，1]时，h（x）＜4等价于g（t）=（2x+1）t+（x-1）²-4＜0，只要

g(0)＜0 g(1)＜0

，即可求实数x的取值范围．

解答： 解：（1）求导可得f′（x）=x²-2bx+c     …1分
∵f′（2-x）=f′（x），∴f′（x）的图象关于直线x=1对称，
∴b=1 …2分
又由已知有：f（3）=0，f′（3）=4，
∴c=1，d=-3  …4分
∴f（x）=

1

3

x³-x²+x-3                …5分
（2）f′（x）=x²-2x+1，
g（x）=x

f′(x)

=x|x-1|=

x2-x，x≥1 x-x2，x＜1

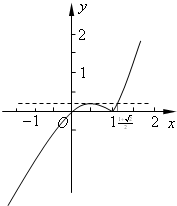
     …7分
其图象如图所示．
当x²-x=

1

4

时，x=

1± 2

2

，根据图象得：
（ⅰ）当0＜m＜

1

2

时，g（x）最大值为m-m²；
（ⅱ）当

1

2

＜m≤

1+ 2

2

时，g（x）最大值为

1

4

；
（ⅲ）当m＞

1+ 2

2

时，g（x）最大值为m²-m．    …10分
（3）h（x）=f′（x）+（2x+1）t=（x-1）²+（2x+1）t，
记g（t）=（2x+1）t+（x-1）²-4，有     …11分
当t∈[0，1]时，h（x）＜4等价于g（t）=（2x+1）t+（x-1）²-4＜0，
∴只要

g(0)＜0 g(1)＜0

，即

(x-1)2-4＜0 2x+1+(x-1)2-4＜0

，
∴-1＜x＜

2

，
∴实数x的取值范围为-1＜x＜

2

，…14分．

点评：本题考查求实数x的取值范围，考查导数知识的综合运用，考查学生分析解决问题的能力，属于中档题．