题目内容
4．在直角坐标系xOy中，曲线C的参数方程为$\left\{\begin{array}{l}{x=\sqrt{3}cosθ}\\{y=sinθ}\end{array}\right.$（θ为参数）．以点O为极点，x轴正半轴为极轴建立极坐标系，直线l的极坐标方程为ρsin（θ+$\frac{π}{4}$）=$\sqrt{2}$．（Ⅰ）将曲线C和直线l化为直角坐标方程；
（Ⅱ）设点Q是曲线C上的一个动点，求它到直线l的距离的最大值．
分析 （Ⅰ）利用三种方程互化方法，将曲线C和直线l化为直角坐标方程；
（Ⅱ）由于点Q是曲线C上的点，则可设点Q的坐标为（$\sqrt{3}$cosθ，sinθ），利用点到直线的距离公式，求它到直线l的距离的最大值．
解答 解：（Ⅰ）由曲线C的参数方程为$\left\{\begin{array}{l}{x=\sqrt{3}cosθ}\\{y=sinθ}\end{array}\right.$（θ为参数）得$\frac{{x}^{2}}{3}+{y}^{2}$=1，
∴曲线C的直角坐标方程为$\frac{{x}^{2}}{3}+{y}^{2}$=1．…（2分）
由ρsin（θ+$\frac{π}{4}$）=$\sqrt{2}$，化简得，ρsinθ+ρcosθ=2，…（4分）
∴x+y=2．
∴直线l的直角坐标方程为x+y=2．…（5分）
（Ⅱ）由于点Q是曲线C上的点，则可设点Q的坐标为（$\sqrt{3}$cosθ，sinθ），…（6分）
点Q到直线l的距离为d=$\frac{|\sqrt{3}cosθ+sinθ-2|}{\sqrt{2}}$…（7分）
=$\frac{|2cos（θ-\frac{π}{6}）-2|}{\sqrt{2}}$．…（8分）
当cos（θ-$\frac{π}{6}$）=-1时，dmax=2$\sqrt{2}$．…（9分）
∴点Q到直线l的距离的最大值为2$\sqrt{2}$．…（10分）
点评 本题考查三种方程的互化，考查点到直线的距离公式的运用，考查参数方程，属于中档题．
练习册系列答案
相关题目
13．已知向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为30°，且|$\overrightarrow{a}$|=$\sqrt{3}$，|$\overrightarrow{b}$|=2，则|$\overrightarrow{a}$-$\overrightarrow{b}$|等于（ ）
| A． | 1 | B． | $\sqrt{13}$ | C． | 13 | D． | $\sqrt{7-2\sqrt{3}}$ |
12．连掷两次骰子分别得到点数m，n，则向量（m，n与向量（-1，1）的夹角θ＞90°的概率是（ ）
| A． | $\frac{5}{12}$ | B． | $\frac{7}{12}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{2}$ |
19．将函数f（x）=xsinx，当${x_1}，{x_2}∈[-\frac{π}{2}，\frac{π}{2}]$时，f（x1）＞f（x2）成立，下列结论正确的是（ ）
| A． | x1＞x2 | B． | x1＞|x2| | C． | x1＜x2 | D． | x${\;}_{1}^{2}$＞x${\;}_{2}^{2}$ |
9．对任意的实数R，集合A={x|x2+x-6＞0}，B={-1，0，1，2，3，4}．则B∩∁RA=（ ）
| A． | {2，3，4，5} | B． | {-1，0} | C． | {-1，0，1，2} | D． | { 2，3，4} |
13．两个整数1908和4187的最大公约数是（ ）
| A． | 53 | B． | 43 | C． | 51 | D． | 67 |
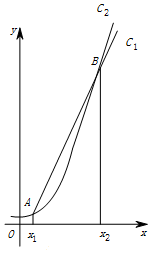函数f（x）=2x和g（x）=x3的图象的示意图如图所示，设两函数的图象交于点A（x1，y1），B（x2，y2），且x1＜x2．若x1∈[a，a+1]，x2∈[b，b+1]，且a，b∈{1，2，3，4，5，6，7，8，9，10，11，12}，则a+b=10．