ƒøƒ⁄»ð
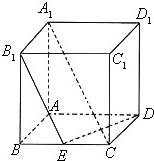 ‘⁄¿‚≥§Œ™2µƒ’˝∑ΩÃÂABCD-A1B1C1D1÷–£¨E «BCµƒ÷–µ„£¨A1D1Ωª∆Ω√ÊB1ED”⁄F£Æ
‘⁄¿‚≥§Œ™2µƒ’˝∑ΩÃÂABCD-A1B1C1D1÷–£¨E «BCµƒ÷–µ„£¨A1D1Ωª∆Ω√ÊB1ED”⁄F£Æ£®1£©÷∏≥ˆF‘⁄A1D1…œµƒŒª÷√£¨≤¢Àµ√˜¿Ì”…£ª
£®2£©“—÷™‘⁄°˜ABC÷–£¨Ω«A£¨B£¨CÀ˘µƒ±þ≥§∑÷±Œ™a£¨b£¨c£¨‘Ú”–“‘œ¬Ω·¬€≥…¡¢£∫
»Ùa2+b2£æc2£¨‘Ú°œC «»ÒΩ«£ª
»Ùa2+b2=c2£¨‘Ú°œC «÷±Ω«£ª
»Ùa2+b2£ºc2£¨‘Ú°œC «∂€Ω«£ª
‘∏˘æð…œ ˆΩ·¬€◊˜≥ˆ“Ï√Ê÷±œþA1C”ÎDEÀ˘≥…µƒΩ«£¨≤¢≈–∂œ∆‰ «∑ÒŒ™÷±Ω«£Æ
øºµ„£∫“Ï√Ê÷±œþº∞∆‰À˘≥…µƒΩ«
◊®Ã‚£∫ø’º‰Ω«
∑÷Œˆ£∫£®1£©◊˜Õº∫Û£®1£©F‘⁄A1D1…œµƒ÷–µ„£ª÷ª–Ë÷§√˜Àƒ±þ–ŒB1FDEŒ™∆Ω––Àƒ±þ–Œ£¨º¥ø…£Æ
£®2£©∏˘æð“Ï√Ê÷±œþÀ˘≥…Ω«µƒ∂®“º¥ø…µ√µΩΩ·¬€£Æ
£®2£©∏˘æð“Ï√Ê÷±œþÀ˘≥…Ω«µƒ∂®“º¥ø…µ√µΩΩ·¬€£Æ
Ω‚¥£∫
 Ω‚£∫£®1£©FŒ™A1D1…œµƒ÷–µ„£Æ
Ω‚£∫£®1£©FŒ™A1D1…œµƒ÷–µ„£Æ
÷§√˜»Áœ¬£∫»°A1D1…œµƒ÷–µ„F£¨¡¨Ω”DF£¨ED£¨
°þ°˜B1A1F°’°˜DCE£¨°˜DD1F°’°˜B1BE£¨
°ýB1F=ED£¨B1=FD£¨
°ýÀƒ±þ–ŒB1FDEŒ™∆Ω––Àƒ±þ–Œ£¨
°ý∆Ω√ÊB1EDΩªA1D1”⁄A1D1µƒ÷–µ„F
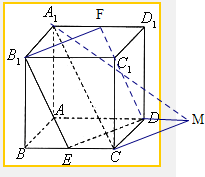
£®2£©—”≥§ADµΩM£¨»°DM=EC£¨
¡¨Ω·A1M”ÎCM£¨
‘ÚDE°ŒCM£¨
‘ÚCM”ÎA1CÀ˘≥…µƒΩ«º¥ø…“Ï√Ê÷±œþA1C”ÎDEÀ˘≥…µƒΩ«£¨
°þ’˝∑Ωõƒ¿‚≥§Œ™2£¨
°ýA1C=2
£¨CM=
=
£¨A1M=
=
£¨
°þCM2+A1C2=17°ŸA1M2£¨
°ý“Ï√Ê÷±œþA1C”ÎDEÀ˘≥…µƒΩ«≤ª «÷±Ω«£Æ
 Ω‚£∫£®1£©FŒ™A1D1…œµƒ÷–µ„£Æ
Ω‚£∫£®1£©FŒ™A1D1…œµƒ÷–µ„£Æ÷§√˜»Áœ¬£∫»°A1D1…œµƒ÷–µ„F£¨¡¨Ω”DF£¨ED£¨
°þ°˜B1A1F°’°˜DCE£¨°˜DD1F°’°˜B1BE£¨
°ýB1F=ED£¨B1=FD£¨
°ýÀƒ±þ–ŒB1FDEŒ™∆Ω––Àƒ±þ–Œ£¨
°ý∆Ω√ÊB1EDΩªA1D1”⁄A1D1µƒ÷–µ„F
£®2£©—”≥§ADµΩM£¨»°DM=EC£¨
¡¨Ω·A1M”ÎCM£¨
‘ÚDE°ŒCM£¨
‘ÚCM”ÎA1CÀ˘≥…µƒΩ«º¥ø…“Ï√Ê÷±œþA1C”ÎDEÀ˘≥…µƒΩ«£¨
°þ’˝∑Ωõƒ¿‚≥§Œ™2£¨
°ýA1C=2
| 3 |
| 22+1 |
| 5 |
| 22+32 |
| 13 |
°þCM2+A1C2=17°ŸA1M2£¨
°ý“Ï√Ê÷±œþA1C”ÎDEÀ˘≥…µƒΩ«≤ª «÷±Ω«£Æ
µ„∆¿£∫±æÂ÷˜“™øº≤È“Ï√Ê÷±œþÀ˘≥…Ω«µƒ∂®“£¨¿˚”√∆Ω––œþ◊™ªØŒ™∆Ω√ÊΩ« «Ω‚戱浃πÿº¸£Æ

¡∑œ∞≤·œµ¡–¥∞∏
œýπÿƒø