题目内容
已知函数f(x)=2cos2x-2
sinxcosx.
(1)求函数f(x)的最小正周期及单调递减区间;
(2)在△ABC中,若f(C)=-1,若sinA,sinC,sinB成等比数列,
•(
-
)=18,求c的值.
| 3 |
(1)求函数f(x)的最小正周期及单调递减区间;
(2)在△ABC中,若f(C)=-1,若sinA,sinC,sinB成等比数列,
| CA |
| AB |
| AC |
考点:两角和与差的正弦函数,平面向量数量积的运算,三角函数的周期性及其求法
专题:三角函数的求值,三角函数的图像与性质,解三角形,平面向量及应用
分析:(1)首先通过三角恒等变换,把函数变形成正弦型函数,进一步求出函数的最小正周期和单调区间.
(2)利用(1)的结论,先求出C的值,进一步利用向量的数量积和余弦定理及等比中项求出结果.
(2)利用(1)的结论,先求出C的值,进一步利用向量的数量积和余弦定理及等比中项求出结果.
解答:
解:(1)函数f(x)=2cos2x-2
sinxcosx=cos2x-
sin2x+1
=2cos(2x+
)+1
∴T=
=π.
令:2kπ≤2x+
≤2kπ+π(k∈Z).
解得:kπ-
≤x≤kπ+
,
函数的单调递减区间为:x∈[kπ-
,kπ+
](k∈Z).
(2)由于f(x)=2cos(2x+
)+1
所以:f(C)=2cos(2C+
)+1=-1
解得:cos(2C+
)=-1,
由于:0<C<π,
所以:
<2C+
<
,
解得:C=
.
由于:sinA,sinC,sinB成等比数列
所以:c2=ab
又
•(
-
)=18
利用向量的数量积:b2-bccosA=18
整理得:a2+b2-c2=36
所以:ab=36
进一步求得:c=6
| 3 |
| 3 |
=2cos(2x+
| π |
| 3 |
∴T=
| 2π |
| 2 |
令:2kπ≤2x+
| π |
| 3 |
解得:kπ-
| π |
| 6 |
| π |
| 3 |
函数的单调递减区间为:x∈[kπ-
| π |
| 6 |
| π |
| 3 |
(2)由于f(x)=2cos(2x+
| π |
| 3 |
所以:f(C)=2cos(2C+
| π |
| 3 |
解得:cos(2C+
| π |
| 3 |
由于:0<C<π,
所以:
| π |
| 3 |
| π |
| 3 |
| 7π |
| 3 |
解得:C=
| π |
| 3 |
由于:sinA,sinC,sinB成等比数列
所以:c2=ab
又
| CA |
| AB |
| AC |
利用向量的数量积:b2-bccosA=18
整理得:a2+b2-c2=36
所以:ab=36
进一步求得:c=6
点评:本题考查的知识要点:三角函数的恒等变换,正弦型函数的周期和单调区间,向量的数量积,余弦定理的应用,等比数列的应用.属于基础题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知a∈R,“实系数一元二次方程x2+ax+
=0的两根都是虚数”是“存在复数z同时满足|z|=2且|z+a|=1”的( )条件.
| 9 |
| 4 |
| A、充分非必要 |
| B、必要非充分 |
| C、充分必要 |
| D、既非充分又非必要 |
函数f(x)=
x+lnx的零点所在的区间是( )
| 1 |
| 2 |
| A、(0,1) |
| B、(1,2) |
| C、(2,3) |
| D、(3,4) |
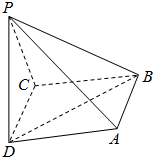 四棱锥P-ABCD的底面是边长为2的正方形,PC=2,PC⊥BC,异面直线AB与PC所成的角为60°.
四棱锥P-ABCD的底面是边长为2的正方形,PC=2,PC⊥BC,异面直线AB与PC所成的角为60°. 如图,在四面体ABCD中,平面ABC⊥平面BCD,AB⊥AC,DC⊥BC,求证:平面ABD⊥平面ACD.
如图,在四面体ABCD中,平面ABC⊥平面BCD,AB⊥AC,DC⊥BC,求证:平面ABD⊥平面ACD.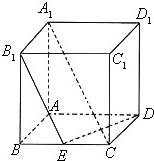 在棱长为2的正方体ABCD-A1B1C1D1中,E是BC的中点,A1D1交平面B1ED于F.
在棱长为2的正方体ABCD-A1B1C1D1中,E是BC的中点,A1D1交平面B1ED于F.