题目内容
已知椭圆
+
=1的左右顶点分别为A,B,点P在椭圆上运动,直线PA与y轴交于点D,则kPA2+2kBD的取值范围为 .
| x2 |
| 4 |
| y2 |
| 3 |
考点:椭圆的简单性质
专题:计算题,直线与圆,圆锥曲线的定义、性质与方程
分析:椭圆
+
=1的左右顶点分别为A(-2,0),B(2,0),设点P(2cosα,
sinα),D(0,t),运用直线的斜率公式,再令t=
,运用二倍角公式,可得t的范围,则kPA2+2kBD=
t2-t=
(t-2)2-1,由t的范围,即可得到所求范围.
| x2 |
| 4 |
| y2 |
| 3 |
| 3 |
| ||
| 1+cosα |
| 1 |
| 4 |
| 1 |
| 4 |
解答:
解:椭圆
+
=1的左右顶点分别为A(-2,0),B(2,0),
设点P(2cosα,
sinα),D(0,t),(t≥0)
则kPA=
∈[0,
],
由P,A,D共线,可得
=
,解得,t=
∈[0,
],
即有D(0,
),kBD=
,
则kPA2+2kBD=
t2-t=
(t-2)2-1,
则[0,
]为递减区间,
t=0时,取得最大值0,t=
时,取得最小值
-
.
所求取值范围是[
-
,0]
故答案为:[
-
,0].
| x2 |
| 4 |
| y2 |
| 3 |
设点P(2cosα,
| 3 |
则kPA=
| ||
| 2(cosα+1) |
| ||
| 2 |
由P,A,D共线,可得
| t |
| 2 |
| ||
| 2(cosα+1) |
| ||
| 1+cosα |
| 3 |
即有D(0,
| ||
| 1+cosα |
| ||
| -2(1+cosα) |
则kPA2+2kBD=
| 1 |
| 4 |
| 1 |
| 4 |
则[0,
| 3 |
t=0时,取得最大值0,t=
| 3 |
| 3 |
| 4 |
| 3 |
所求取值范围是[
| 3 |
| 4 |
| 3 |
故答案为:[
| 3 |
| 4 |
| 3 |
点评:本题考查椭圆的参数方程及应用,考查直线的斜率公式的运用,考查二次函数的最值,属于中档题.

练习册系列答案
相关题目
函数f(x)=
x+lnx的零点所在的区间是( )
| 1 |
| 2 |
| A、(0,1) |
| B、(1,2) |
| C、(2,3) |
| D、(3,4) |
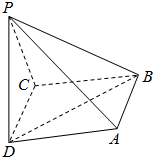 四棱锥P-ABCD的底面是边长为2的正方形,PC=2,PC⊥BC,异面直线AB与PC所成的角为60°.
四棱锥P-ABCD的底面是边长为2的正方形,PC=2,PC⊥BC,异面直线AB与PC所成的角为60°.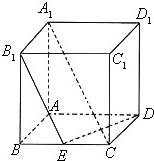 在棱长为2的正方体ABCD-A1B1C1D1中,E是BC的中点,A1D1交平面B1ED于F.
在棱长为2的正方体ABCD-A1B1C1D1中,E是BC的中点,A1D1交平面B1ED于F.