题目内容

设向量
a
、
b
不共线，向量
c
=λ
a
+μ
b
，且
a
、
b
、
c
有共同的起点0，λ+μ=1，试证：
a
、
b
、
c
的终点在同一条直线上．
考点：平行向量与共线向量
专题：平面向量及应用
分析：根据题意，只要计算
a
-
c
，与
c
-
b
是共线向量即可．
解答： 解：因为向量
a
、
b
不共线，向量
c
=λ
a
+μ
b
，且
a
、
b
、
c
有共同的起点0，λ+μ=1，
所以
a
-
c
=
a
-λ
a
-μ
b
=(1-λ)
a
-μ
b
=μ
a
-μ
b
=μ(
a
-
b
)；
c
-
b
=λ
a
+μ
b
-
b
=λ
a
+(μ-1)
b
=λ
a
-λ
b
=λ(
a
-
b
)=
λ
μ
(
a
-
c
)，
所以
a
-
c
，与
c
-
b
是共线向量，
所以
a
、
b
、
c
的终点在同一条直线上．
点评：若
OC
=λ
OA
+μ
OB
，且λ+μ=1．则A、B、C三点共线，且C分AB的两段线段AC与BC的长度之比，AC：BC=μ：λ．
练习册系列答案
相关题目
设函数f（x）=lnx+
m
x
，m∈R．
（1）若函数g（x）=f′（x）-
x
3
只有一个零点，求m的取值范围；
（2）若对于任意b＞a＞0，
f(b)-f(a)
b-a
＜1恒成立，求m的取值范围．
已知函数f（x）=log2a-1（2x+1），在区间（
3
2
，+∞）上满足f（x）＞0，试求实数a的取值范围．
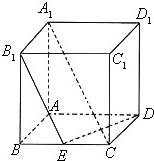在棱长为2的正方体ABCD-A1B1C1D1中，E是BC的中点，A1D1交平面B1ED于F．
（1）指出F在A1D1上的位置，并说明理由；
（2）已知在△ABC中，角A，B，C所的边长分别为a，b，c，则有以下结论成立：
若a2+b2＞c2，则∠C是锐角；
若a2+b2=c2，则∠C是直角；
若a2+b2＜c2，则∠C是钝角；
试根据上述结论作出异面直线A1C与DE所成的角，并判断其是否为直角．
已知非零向量
AB
、
AC
满足
AB
|
AB|
+
AC
|
AC
|
=λ（
AB
+
AC
），（λ＞0）且
AB
|
AB|
•
AC
|
AC
|
=
1
2
，
BC
=2，则△ABC的周长为
 
．
求函数f（x）=sinx+
1
2
x，x∈（0，2π）的极值．
已知四边形ABCD是平行四边形，点O是空间任意一点，设
OA
=
a
，
OB
=
b
，
OC
=
c
，则向量
OD
用
a
、
b
、
c
表示为（　　）
A、
a
-
b
-
c
B、
a
-
b
+
c
C、-
a
-
b
+
c
D、-
a
+
b
+
c
某企业拟在2014年度进行一系列促销活动，已知其产品年销量x万件与年促销费用t万元之间满足3-x与t+1成反比例，当年促销费用t=0万元时，年销量是1万件．已知2014年产品的设备折旧、维修等固定费用为3万元，每生产1万件产品需再投入32万元的生产费用，若将每件产品售价定为：其生产成本的150%与“平均每件促销费的一半”之和，则当年生产的商品正好能销完．
（Ⅰ）将2014年的利润y（万元）表示为促销费t（万元）的函数；
（Ⅱ）该企业2014年的促销费投入多少万元时，企业年利润最大？
（注：利润=销售收入-生产成本-促销费，生产成本=固定费用+生产费用）
已知椭圆
x2
5
+y2=1，椭圆的中心为坐标原点O，点F是椭圆的右焦点，点A是椭圆短轴的一个端点，过点F的直线l与椭圆交于M、N两点，与OA所在直线交于E点，若
EM
=λ1
MF
，
EN
=λ2
NF
，则λ1+λ2=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网