题目内容
已知曲线C上任意一点到两定点O(0,0)和A(3,0)的距离之比为
=
,
(1)求曲线C的方程;
(2)过(0,2)点的直线l被曲线C截得的弦长为2
,求l的方程.
| |MO| |
| |MA| |
| 1 |
| 2 |
(1)求曲线C的方程;
(2)过(0,2)点的直线l被曲线C截得的弦长为2
| 3 |
考点:轨迹方程,直线与圆锥曲线的关系
专题:综合题,直线与圆
分析:(1)设M的坐标为(x,y),由题意动点M到定点O(0,0)和A(3,0)的距离之比为
=
,结合两点间的距离,化简整理得动点M轨迹C的方程;
(2)分类讨论,利用点N的直线l被曲线C截得的弦长为2
,即可求直线l的方程.
| |MO| |
| |MA| |
| 1 |
| 2 |
(2)分类讨论,利用点N的直线l被曲线C截得的弦长为2
| 3 |
解答:
解:(1)设M的坐标为(x,y),由题意,
∵动点M到定点O(0,0)和A(3,0)的距离之比为
=
,
∴
=
,
整理得x2+y2+2x-3=0;
(2)x2+y2+2x-3=0可化为(x+1)2+y2=4,
斜率不存在时,直线方程为x=0,y=±
,满足题意;
斜率存在时,设方程为y=kx+2,
∵过(0,2)点的直线l被曲线C截得的弦长为2
,
∴圆心到直线的距离为1,
∴
=1,
∴k=
,
∴直线l的方程为y=
x+2.
综上,直线l的方程为y=
x+2或x=0.
∵动点M到定点O(0,0)和A(3,0)的距离之比为
| |MO| |
| |MA| |
| 1 |
| 2 |
∴
| x2+y2 |
| (x-3)2+y2 |
| 1 |
| 4 |
整理得x2+y2+2x-3=0;
(2)x2+y2+2x-3=0可化为(x+1)2+y2=4,
斜率不存在时,直线方程为x=0,y=±
| 3 |
斜率存在时,设方程为y=kx+2,
∵过(0,2)点的直线l被曲线C截得的弦长为2
| 3 |
∴圆心到直线的距离为1,
∴
| |-k+2| | ||
|
∴k=
| 3 |
| 4 |
∴直线l的方程为y=
| 3 |
| 4 |
综上,直线l的方程为y=
| 3 |
| 4 |
点评:本题考查直线的方程,注意结合题意,选择直线方程的合适的形式,进行整理变形、求解.

练习册系列答案
相关题目
函数f(x)=
x+lnx的零点所在的区间是( )
| 1 |
| 2 |
| A、(0,1) |
| B、(1,2) |
| C、(2,3) |
| D、(3,4) |
已知四边形ABCD是平行四边形,点O是空间任意一点,设
=
,
=
,
=
,则向量
用
、
、
表示为( )
| OA |
| a |
| OB |
| b |
| OC |
| c |
| OD |
| a |
| b |
| c |
A、
| ||||||
B、
| ||||||
C、-
| ||||||
D、-
|
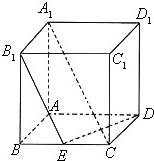 在棱长为2的正方体ABCD-A1B1C1D1中,E是BC的中点,A1D1交平面B1ED于F.
在棱长为2的正方体ABCD-A1B1C1D1中,E是BC的中点,A1D1交平面B1ED于F.