题目内容
已知
=(1,x),
=(x2+x,-x),解关于x的不等式
•
+2>m(
+1)(其中m是满足m≤-2的常数).
| a |
| b |
| a |
| b |
| 2 | ||||
|
考点:平面向量数量积的运算
专题:平面向量及应用
分析:
•
=x2+x-x2=x,不等式
•
+2>m(
+1)化为x+2>m(
+1),即x(x+2)(x-m)>0,对m分类讨论即可解出.
| a |
| b |
| a |
| b |
| 2 | ||||
|
| 2 |
| x |
解答:
解:
•
=x2+x-x2=x,
∴不等式
•
+2>m(
+1)化为x+2>m(
+1),
∴
>0,
∴x(x+2)(x-m)>0,
当m=-2时,化为x(x+2)2>0,解得x>0.
当m<-2时,解得x>0或m<x<-2.
综上可得:当m=-2时,不等式的解集为{x|x>0}.
当m<-2时,不等式的解集为{x|x>0或m<x<-2}.
| a |
| b |
∴不等式
| a |
| b |
| 2 | ||||
|
| 2 |
| x |
∴
| (x+2)(x-m) |
| x |
∴x(x+2)(x-m)>0,
当m=-2时,化为x(x+2)2>0,解得x>0.
当m<-2时,解得x>0或m<x<-2.
综上可得:当m=-2时,不等式的解集为{x|x>0}.
当m<-2时,不等式的解集为{x|x>0或m<x<-2}.
点评:本题考查了向量的数量积运算、不等式的解法、分类讨论思想方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
已知四边形ABCD是平行四边形,点O是空间任意一点,设
=
,
=
,
=
,则向量
用
、
、
表示为( )
| OA |
| a |
| OB |
| b |
| OC |
| c |
| OD |
| a |
| b |
| c |
A、
| ||||||
B、
| ||||||
C、-
| ||||||
D、-
|
 如图,在四面体ABCD中,平面ABC⊥平面BCD,AB⊥AC,DC⊥BC,求证:平面ABD⊥平面ACD.
如图,在四面体ABCD中,平面ABC⊥平面BCD,AB⊥AC,DC⊥BC,求证:平面ABD⊥平面ACD.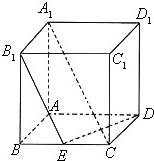 在棱长为2的正方体ABCD-A1B1C1D1中,E是BC的中点,A1D1交平面B1ED于F.
在棱长为2的正方体ABCD-A1B1C1D1中,E是BC的中点,A1D1交平面B1ED于F.