题目内容
已知椭圆C:
+
=1,试确定m的取值范围,使得对于直线l:y=4x+m,椭圆C上有两个不同的点关于直线l对称.
| x2 |
| 4 |
| y2 |
| 3 |
考点:直线与圆锥曲线的关系
专题:圆锥曲线中的最值与范围问题
分析:第一步:设椭圆上关于直线l对称的两点分别为A(x1,y1),B(x2,y2),AB的中点为M(x0,y0);
第二步:将A,B两点坐标代入椭圆方程中,由点差法得AB的斜率kAB与中点坐标(x0,y0)的关系式,又由l⊥AB,得x0与y0的关系;
第三步:将坐标(x0,y0) 代入l的方程中,得x0与y0的另一个关系;
第四步:由第二、三步的两个关系式,可将x0,y0用m表示;
第五步:将x0,y0代入椭圆方程的左边,根据M在椭圆内部,得到关于m的不等式,解此不等式即可.
第二步:将A,B两点坐标代入椭圆方程中,由点差法得AB的斜率kAB与中点坐标(x0,y0)的关系式,又由l⊥AB,得x0与y0的关系;
第三步:将坐标(x0,y0) 代入l的方程中,得x0与y0的另一个关系;
第四步:由第二、三步的两个关系式,可将x0,y0用m表示;
第五步:将x0,y0代入椭圆方程的左边,根据M在椭圆内部,得到关于m的不等式,解此不等式即可.
解答:
解:设椭圆上关于直线l对称的两点分别为A(x1,y1),B(x2,y2),
AB的中点为M(x0,y0),
则由
,两式相减得
+
=0,
即
+
=0,
又由直线AB的斜率kAB=
,以及中点公式
,
得
+
•kAB=0,即kAB=-
,又由l⊥AB,得kAB=-
,
∴-
=-
,即y=3x.…①
∵点M在直线l上,∴y0=4x0+m.…②
联立①、②,得
,即M(-m,-3m),
根据点M在椭圆的内部,得
+
<1,
解得-
<m<
.
AB的中点为M(x0,y0),
则由
|
| ||||
| 4 |
| ||||
| 3 |
即
| (x1+x2)(x1-x2) |
| 4 |
| (y1+y2)(y1-y2) |
| 3 |
又由直线AB的斜率kAB=
| y1-y2 |
| x1-x2 |
|
得
| x0 |
| 4 |
| y0 |
| 3 |
| 3x0 |
| 4y0 |
| 1 |
| 4 |
∴-
| 3x0 |
| 4y0 |
| 1 |
| 4 |
∵点M在直线l上,∴y0=4x0+m.…②
联立①、②,得
|
根据点M在椭圆的内部,得
| (-m)2 |
| 4 |
| (-3m)2 |
| 3 |
解得-
2
| ||
| 13 |
2
| ||
| 13 |
点评:本题考查了直线与椭圆的相交关系,点关于直线的对称性,参数范围的求解等,关键是通过消参,找到参数m与中点坐标x0,y0的关系,处理参数范围问题的一般步骤是:
1、设参;
2、建立等量关系,并消去多余参数;
3、寻找不等关系,解不等式.
1、设参;
2、建立等量关系,并消去多余参数;
3、寻找不等关系,解不等式.

练习册系列答案
相关题目
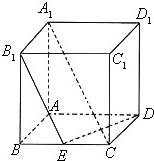 在棱长为2的正方体ABCD-A1B1C1D1中,E是BC的中点,A1D1交平面B1ED于F.
在棱长为2的正方体ABCD-A1B1C1D1中,E是BC的中点,A1D1交平面B1ED于F. 如图,M,N分别是空间四边形ABCD的棱AB,CD的中点,试判断向量
如图,M,N分别是空间四边形ABCD的棱AB,CD的中点,试判断向量