题目内容
已知定义在R上的函数f(x)满足f(x)=
且f(x)=f(x+2),函数g(x))的表达式为g(x)=
,则方程g(x)=f(x)在区间[-5,1]上的所有实数根之和为 .
|
| x+3 |
| x+2 |
考点:函数的零点与方程根的关系
专题:计算题,函数的性质及应用
分析:由题意,函数f(x)是周期函数,从而讨论每一段上的函数值,从而求方程g(x)=f(x)的解.
解答:
解:由题意,当x=1时,f(1)=f(-1)=0,g(1)=
;
当0≤x<1时,x2+1=
,
即(x+1)(x2+x-1)=0,
解得x=
;
当-1≤x<0时,f(x)<1,
g(x)>1,无解;
当-2<x<-1时,f(x)<2,
g(x)>2,无解;
当-3≤x<-2时,f(x)>0,
g(x)<0,无解;
当-4≤x<-3时,f(x)=f(x+4)=(x+4)2+1>1,
g(x)<1,无解;
当-5≤x<-4时,f(x)=f(x+4)=1-(x+4)2<1,
g(x)<1,
则1-(x+4)2=
,
解得x=
;
则
+
=-4;
故答案为:-4.
| 4 |
| 3 |
当0≤x<1时,x2+1=
| x+3 |
| x+2 |
即(x+1)(x2+x-1)=0,
解得x=
-1+
| ||
| 2 |
当-1≤x<0时,f(x)<1,
g(x)>1,无解;
当-2<x<-1时,f(x)<2,
g(x)>2,无解;
当-3≤x<-2时,f(x)>0,
g(x)<0,无解;
当-4≤x<-3时,f(x)=f(x+4)=(x+4)2+1>1,
g(x)<1,无解;
当-5≤x<-4时,f(x)=f(x+4)=1-(x+4)2<1,
g(x)<1,
则1-(x+4)2=
| x+3 |
| x+2 |
解得x=
-7-
| ||
| 2 |
则
-7-
| ||
| 2 |
-1+
| ||
| 2 |
故答案为:-4.
点评:本题考查了函数的周期性的应用及分段函数的函数值,属于难题.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案
相关题目
已知a∈R,“实系数一元二次方程x2+ax+
=0的两根都是虚数”是“存在复数z同时满足|z|=2且|z+a|=1”的( )条件.
| 9 |
| 4 |
| A、充分非必要 |
| B、必要非充分 |
| C、充分必要 |
| D、既非充分又非必要 |
函数f(x)=
x+lnx的零点所在的区间是( )
| 1 |
| 2 |
| A、(0,1) |
| B、(1,2) |
| C、(2,3) |
| D、(3,4) |
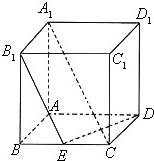 在棱长为2的正方体ABCD-A1B1C1D1中,E是BC的中点,A1D1交平面B1ED于F.
在棱长为2的正方体ABCD-A1B1C1D1中,E是BC的中点,A1D1交平面B1ED于F.