题目内容
3.对于函数f(x)=$\frac{2}{{3}^{x}+1}$+m,(m∈R)(1)判断函数f(x)的单调性,并用定义证明
(2)是否存在实数m使函数f(x)为奇函数.
分析 (1)利用函数单调性的定义,即可证明;
(2)利用f(0)=0,即可求解.
解答 解:(1)f(x) 在(-∞,+∞) 上为单调减函数
证明:设x1>x2,则:f(x1)-f(x2)=$\frac{2({3}^{{x}_{2}}-{3}^{{x}_{1}})}{({3}^{{x}_{1}}+1)({3}^{{x}_{2}}+1)}$
∵x1>x2;
∴${3}^{{x}_{2}}$-${3}^{{x}_{1}}$<0,∴f(x1)<f(x2),
∴f(x) 在 (-∞,+∞) 上为减函数. (6分)
(2)令f(0)=0,可得1+m=0,∴m=-1.
点评 本题考查根据减函数的定义证明一个函数为减函数的方法及过程,考查函数的奇偶性,属于中档题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
8.设直线l经过椭圆$\frac{x^2}{4}+{y^2}=1$的右焦点且倾斜角为45°,若直线l与椭圆相交于A,B两点,则|AB|=( )
| A. | $\frac{2}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{6}{5}$ | D. | $\frac{8}{5}$ |
13.已知正六棱柱的12个顶点都在一个半径为3的球面上,当正六棱柱的体积最大时,其高的值为( )
| A. | 3$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{6}$ | D. | 2$\sqrt{3}$ |
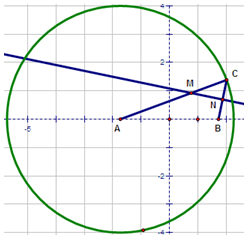 以$A(-\sqrt{3},0)$为圆心,4为半径作圆,$B(\sqrt{3},0)$,C为圆上任意一点,分别连接AC,BC,过BC的中点N作BC的垂线,交AC于点M,当点C在圆上运动时,
以$A(-\sqrt{3},0)$为圆心,4为半径作圆,$B(\sqrt{3},0)$,C为圆上任意一点,分别连接AC,BC,过BC的中点N作BC的垂线,交AC于点M,当点C在圆上运动时, 如图,四棱锥P-ABCD中,AD∥BC,AD⊥DC,AD=2BC=2CD=2,侧面APD为等腰直角三角形,∠APD=90°,平面PAD⊥平面ABCD,E为棱PC上的一点.
如图,四棱锥P-ABCD中,AD∥BC,AD⊥DC,AD=2BC=2CD=2,侧面APD为等腰直角三角形,∠APD=90°,平面PAD⊥平面ABCD,E为棱PC上的一点.