题目内容
13．
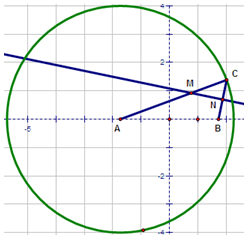以$A（-\sqrt{3}，0）$为圆心，4为半径作圆，$B（\sqrt{3}，0）$，C为圆上任意一点，分别连接AC，BC，过BC的中点N作BC的垂线，交AC于点M，当点C在圆上运动时，（1）求M点的轨迹方程，并说明它是何种曲线；
（2）求直线y=kx+1截（1）所得曲线弦长的最大值．
分析 （1）利用椭圆的定义求M点的轨迹方程，并说明它是何种曲线；
（2）直线y=kx+1代入椭圆方程，可得（1+4k2）x2+8kx=0，表示出弦长，即可求直线y=kx+1截（1）所得曲线弦长的最大值．
解答 解：（1）由题意，|MA|+|MB|=|AC|=4＞2$\sqrt{3}$，
∴M点的轨迹是以A，B为焦点的椭圆，a=2，c=$\sqrt{3}$，
∴b=1，
∴椭圆方程为$\frac{{x}^{2}}{4}+{y}^{2}$=1；
（2）直线y=kx+1代入椭圆方程，可得（1+4k2）x2+8kx=0，
∴x=0或x=-$\frac{8k}{1+4{k}^{2}}$，
∴弦长L=$\sqrt{1+{k}^{2}}•|\frac{8k}{1+4{k}^{2}}|$，
设t=1+4k2（t≥1），则L2=-12（$\frac{1}{t}$-$\frac{1}{3}$）2+$\frac{16}{3}$，
∴t=3时，L的最大值为$\frac{4\sqrt{3}}{3}$．
点评 本题考查轨迹方程，考查直线与椭圆的位置关系，考查弦长的计算，属于中档题．
练习册系列答案
相关题目
4．下列关系中正确的个数为（ ）
①0∈{0}
②Φ?{0}
③{0，1}⊆{（0，1）}．
①0∈{0}
②Φ?{0}
③{0，1}⊆{（0，1）}．
| A． | 0 | B． | 1 | C． | 2 | D． | 3 |
1．焦点在x轴上的椭圆${x^2}-\frac{y^2}{k}=1$的离心率为$\frac{1}{2}$，则焦距为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{{\sqrt{2}}}{2}$ | C． | $\sqrt{2}$ | D． | 1 |
某电视台组织部分记者，用“10分制”随机调查某社区居民的幸福指数，现从调查人群中随机抽取16名，如图所示的茎叶图记录了他们的幸福指数的得分（以小数点的前一位数字为茎，小数点后的一位数字为叶）：