题目内容
11.已知函数f(x)=ax2+bx+c的图象在y轴上的截距为1,且满足f(x+1)=f(x)+x+1,试求:(1)f(x)的解析式;
(2)当f(x)≤7时,对应的x的取值范围.
分析 (1)利用函数的截距求出c,利用待定系数法求解a,b即可.
(2)转化不等式,通过二次不等式求解即可.
解答 解:(1)函数f(x)=ax2+bx+c的图象在y轴上的截距为1,可得c=1;
f(x+1)=f(x)+x+1,
可得:a(x+1)2+bx+b+1=ax2+bx+x+2;
可得:$\left\{\begin{array}{l}{a+b+1=2}\\{2a+b=b+1}\end{array}\right.$解得a=$\frac{1}{2}$,b=$\frac{1}{2}$.
可得函数的解析式为:f(x)=$\frac{1}{2}$x2+$\frac{1}{2}$x+1.
(2)f(x)≤7,可得:$\frac{1}{2}$x2+$\frac{1}{2}$x+1≤7,
可得x2+x-12≤0,
解得-4≤x≤3.
点评 本题考查二次函数的简单性质,考查转化思想以及计算能力.

练习册系列答案
相关题目
1.焦点在x轴上的椭圆${x^2}-\frac{y^2}{k}=1$的离心率为$\frac{1}{2}$,则焦距为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | 1 |
19.不等式x2+ax-b<0的解集是(2,3),则bx2-ax-1>0的解集是( )
| A. | $(\frac{1}{3},\frac{1}{2})$ | B. | $(\frac{1}{6},1)$ | C. | $(-\frac{1}{2},-\frac{1}{3})$ | D. | $(-∞,-\frac{1}{2})∪(-\frac{1}{3},+∞)$ |
6.如果函数f(x)=(a2-1)x在R上是减函数,那么实数a的取值范围是( )
| A. | |a|>1 | B. | |a|<2 | C. | |a|>3 | D. | 1<|a|<$\sqrt{2}$ |
1.已知球O的内接圆柱的体积是2π,底面半径为1,则球O的表面积为( )
| A. | 6π | B. | 8π | C. | 10π | D. | 12π |
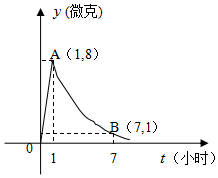 某医药研究所开发一种新药,据监测,如果成人按规定的剂量服用,服用药后每毫升中的含药量y(微克)与服药的时间t(小时)之间近似满足如图所示的曲线,其中OA是线段,曲线AB是函数y=kat(t≥1,a>0,且k,a是常数)的图象.
某医药研究所开发一种新药,据监测,如果成人按规定的剂量服用,服用药后每毫升中的含药量y(微克)与服药的时间t(小时)之间近似满足如图所示的曲线,其中OA是线段,曲线AB是函数y=kat(t≥1,a>0,且k,a是常数)的图象.