题目内容
14.在数列{an}中,a1=1,a2=2,且an+1=(1+q)an-qan-1(n≥2,q≠0)(Ⅰ)设bn=an+1-an(n∈N*),证明{bn}是等比数列;
(Ⅱ)当q=2时,求数列{an}的通项公式.
分析 (Ⅰ)推导出bn=an+1-an=qbn-1,n≥2,b1=a2-a1=1,q≠0,由此能证明{bn}是首项为1,公比为q的等比数列.
(Ⅱ)由a2-a1=1,a3-a2=q,…,${a}_{n}-{a}_{n-1}={q}^{n-2}$,利用累加法能求出数列{an}的通项公式.
解答 证明:(Ⅰ)∵数列{an}中,a1=1,a2=2,且an+1=(1+q)an-qan-1(n≥2,q≠0),
∴an+1-an=q(an-an-1),即bn=an+1-an=qbn-1,n≥2,
又b1=a2-a1=1,q≠0,
∴{bn}是首项为1,公比为q的等比数列.
解:(Ⅱ)由(Ⅰ)得a2-a1=1,a3-a2=q,
…,${a}_{n}-{a}_{n-1}={q}^{n-2}$,
将以上各式相加,得:
an-a1=1+q+…+qn-1=1+2+…+2n-2=$\frac{1-{2}^{n-1}}{1-2}$=2n-1-1.
∴an=2n-1.
n=1时,上式也成立,
∴数列{an}的通项公式an=2n-1.
点评 本题考查等比数列的证明,考查数列的通项公式的求法,是中档题,解题时要认真审题,注意累加法的合理运用.

练习册系列答案
相关题目
4.下列关系中正确的个数为( )
①0∈{0}
②Φ?{0}
③{0,1}⊆{(0,1)}.
①0∈{0}
②Φ?{0}
③{0,1}⊆{(0,1)}.
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
19.不等式x2+ax-b<0的解集是(2,3),则bx2-ax-1>0的解集是( )
| A. | $(\frac{1}{3},\frac{1}{2})$ | B. | $(\frac{1}{6},1)$ | C. | $(-\frac{1}{2},-\frac{1}{3})$ | D. | $(-∞,-\frac{1}{2})∪(-\frac{1}{3},+∞)$ |
6.如果函数f(x)=(a2-1)x在R上是减函数,那么实数a的取值范围是( )
| A. | |a|>1 | B. | |a|<2 | C. | |a|>3 | D. | 1<|a|<$\sqrt{2}$ |
4.一个几何体的三视图如图所示,则该几何体的表面积是( )
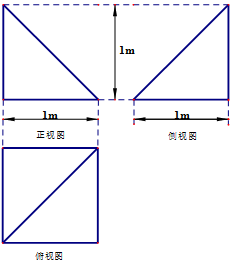

| A. | $(1+\sqrt{2}){m^2}$ | B. | $(1+2\sqrt{2}){m^2}$ | C. | $(2+\sqrt{2}){m^2}$ | D. | $(2+2\sqrt{2}){m^2}$ |