题目内容
已知等比数列{an}的前n项和Sn=(
)n+a,则a的值( )
| 1 |
| 2 |
| A、-1 | ||
| B、1 | ||
C、-
| ||
D、
|
考点:等比数列的前n项和
专题:等差数列与等比数列
分析:由等比数列的前n项和求得数列前三项,然后利用等比数列的性质列式求得a的值.
解答:
解:∵数列{an}是等比数列,且其前n项和Sn=(
)n+a,
则a1=S1=
+a,
a2=S2-S1=(
)2+a-
-a=-
,
a3=S3-S2=(
)3+a-(
)2-a=-
,
由(-
)2=-
(
+a),解得:a=-1.
故选:A.
| 1 |
| 2 |
则a1=S1=
| 1 |
| 2 |
a2=S2-S1=(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
a3=S3-S2=(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 8 |
由(-
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 2 |
故选:A.
点评:本题考查了等比数列的前n项和,考查了等比数列的性质,是基础题.

练习册系列答案
相关题目
已知sinα-cosα=
,则tanα+
=( )
| 1 |
| 3 |
| 1 |
| tanα |
A、
| ||
B、
| ||
C、
| ||
D、
|
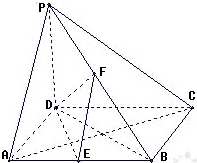 已知四棱锥P-ABCD,底面是边长为a的正方形,PD⊥底面ABCD,PD=DC,E、F分别是AB、PB的中点,
已知四棱锥P-ABCD,底面是边长为a的正方形,PD⊥底面ABCD,PD=DC,E、F分别是AB、PB的中点,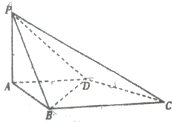 如图,四棱锥P-ABCD的底面ABCD是直角梯形,AD∥BC,∠BAD=90°,PA⊥平面ABCD,且PA=AD=AB=1.
如图,四棱锥P-ABCD的底面ABCD是直角梯形,AD∥BC,∠BAD=90°,PA⊥平面ABCD,且PA=AD=AB=1.