题目内容
已知函数f(x)=log9(9x+1)+kx(k∈R)为偶函数.
(1)求k的值;
(2)解关于x的不等式f(x)-log9(a+
)>0(a>0).
(1)求k的值;
(2)解关于x的不等式f(x)-log9(a+
| 1 |
| a |
考点:函数奇偶性的性质,指、对数不等式的解法
专题:函数的性质及应用
分析:(1)转化为log9
-log9(9x+1)=2kx恒成立求解.(2)利用(3x-a)(3x-
)>0,分类讨论求解.
| 9x+1 |
| 9x |
| 1 |
| a |
解答:
解:(1)∵f(x)为偶函数,
∴f(-x)=f(x),
即log9(9-x+1)-kx=log9(49+1)+kx,
∴log9
-log9(9x+1)=2kx,
∴(2k+1)x=0,∴k=-
,
(2)f(x)-log9(a+
)>0⇒log9(9x+1)-
>log9(a+
)
⇒log9
>log9(a+
)
⇒
>a+
,
⇒(3x)2-(a+
)3x+1>0
⇒(3x-a)(3x-
)>0
( I)①a>1时⇒3x>a或3x<
⇒{x|x>log3a或x<log3
},
②0<a<1时⇒3x>
或3x<a,{x|x>log 3
或x<log3a},
③a=1时⇒3x≠1,{x|x≠0}.
∴f(-x)=f(x),
即log9(9-x+1)-kx=log9(49+1)+kx,
∴log9
| 9x+1 |
| 9x |
∴(2k+1)x=0,∴k=-
| 1 |
| 2 |
(2)f(x)-log9(a+
| 1 |
| a |
| x |
| 2 |
| 1 |
| a |
⇒log9
| 9x+1 | ||
9
|
| 1 |
| a |
⇒
| 9x+1 |
| 3x |
| 1 |
| a |
⇒(3x)2-(a+
| 1 |
| a |
⇒(3x-a)(3x-
| 1 |
| a |
( I)①a>1时⇒3x>a或3x<
| 1 |
| a |
| 1 |
| a |
②0<a<1时⇒3x>
| 1 |
| a |
| 1 |
| a |
③a=1时⇒3x≠1,{x|x≠0}.
点评:本题考查了函数的性质,不等式的解法,属于中档题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
已知函数f(x)=
,则f(
)=( )
|
| 1 |
| 9 |
| A、0 | B、1 | C、3 | D、-2 |
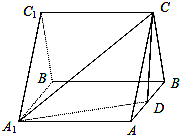 如图,三棱柱ABCA1B1C1中,侧棱A1A⊥底面ABC,且各棱长均相等,D为棱AB的中点.
如图,三棱柱ABCA1B1C1中,侧棱A1A⊥底面ABC,且各棱长均相等,D为棱AB的中点.