题目内容
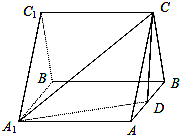 如图,三棱柱ABCA1B1C1中,侧棱A1A⊥底面ABC,且各棱长均相等,D为棱AB的中点.
如图,三棱柱ABCA1B1C1中,侧棱A1A⊥底面ABC,且各棱长均相等,D为棱AB的中点.(1)证明:平面A1CD⊥平面A1ABB1;
(2)求直线BC与平面A1CD所成角的正弦值.
考点:直线与平面所成的角,平面与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(1)通过证明CD⊥AB,AA1⊥CD,推出CD⊥平面A1ABB1,然后利用平面与平面垂直的判定定理证明平面A1CD⊥平面A1ABB1;
(2)过点 B 作 B G⊥A1D交直线A1D于点G,连接CG.说明∠BCG为直线BC与平面A1CD所成的角,通过解三角形求解直线BC与平面A1CD所成角的正弦值.
(2)过点 B 作 B G⊥A1D交直线A1D于点G,连接CG.说明∠BCG为直线BC与平面A1CD所成的角,通过解三角形求解直线BC与平面A1CD所成角的正弦值.
解答:
解:(1)证明:由于底面ABC是正三角形,D为AB的中点,故CD⊥AB,
又侧棱A1A⊥底面ABC,CD?平面ABC,所以AA1⊥CD,又AA1∩AB=A,
因此CD⊥平面A1ABB1,而CD?平面A1CD,
所以平面A1CD⊥平面A1ABB1.
(2)在平面A1ABB1内,过点 B 作 B G⊥A1D交直线A1D于点G,连接CG.
由于平面A1CD⊥平面A1ABB1,而直线A1D是平面A1CD与平面A1ABB1的交线,
故BG⊥平面A1CD.由此得∠BCG为直线BC与平面A1CD所成的角.
设棱长为a,可得A1D=
,则△A1AD∽△BGD,易得BG=
,
在Rt△BGC中,sin∠BCG=
=
.
所以直线BC与平面A1CD所成角的正弦值为
.
又侧棱A1A⊥底面ABC,CD?平面ABC,所以AA1⊥CD,又AA1∩AB=A,
因此CD⊥平面A1ABB1,而CD?平面A1CD,
所以平面A1CD⊥平面A1ABB1.
(2)在平面A1ABB1内,过点 B 作 B G⊥A1D交直线A1D于点G,连接CG.
由于平面A1CD⊥平面A1ABB1,而直线A1D是平面A1CD与平面A1ABB1的交线,
故BG⊥平面A1CD.由此得∠BCG为直线BC与平面A1CD所成的角.
设棱长为a,可得A1D=
| ||
| 2 |
| ||
| 5 |
在Rt△BGC中,sin∠BCG=
| BG |
| BC |
| ||
| 5 |
所以直线BC与平面A1CD所成角的正弦值为
| ||
| 5 |
点评:本题考查平面与平面垂直的判定定理的应用,直线与平面所成角的求法,考查空间想象能力以及逻辑推理能力,计算能力.

练习册系列答案
相关题目
若集合A={x|x>-3},则( )
| A、0⊆A | B、{0}∈A |
| C、∅∈A | D、{0}⊆A |
在△ABC中,角A,B,C所对的边分别是a,b,c,若cosC>
,则△ABC的形状是( )
| b |
| a |
| A、等腰三角形 |
| B、锐角三角形 |
| C、钝角三角形 |
| D、直角三角形 |
设全集U={1,2,3,4,5,6,7,8},集合S={1,3,5},T={3,6},则∁U(S∪T)等于( )
| A、{2,4,7,8} |
| B、∅ |
| C、{1,3,5,6} |
| D、{2,4,6,8} |