题目内容
已知二次函数y=f(x),满足f(1)=3,f(-1)=-1,f(x)的最小值-1.
(Ⅰ)求f(x);
(Ⅱ)若函y=F(x),x∈R为奇函数,x>0时,F(x)=f(x),求函数y=F(x),x∈R的解析式;
(Ⅲ)设g(x)=f(-x)-λf(x)+1,若g(x)在[-1,1]上是减函数,求实数λ的取值范围.
(Ⅰ)求f(x);
(Ⅱ)若函y=F(x),x∈R为奇函数,x>0时,F(x)=f(x),求函数y=F(x),x∈R的解析式;
(Ⅲ)设g(x)=f(-x)-λf(x)+1,若g(x)在[-1,1]上是减函数,求实数λ的取值范围.
考点:二次函数的性质
专题:函数的性质及应用
分析:(Ⅰ)设出函数的解析式,得到方程组,解出即可;
(Ⅱ)结合函数的奇偶性,分别求出各个区间上的函数解析式,综合得出结论;
(Ⅲ)通过讨论λ的范围,结合函数的单调性,从而得出结论.
(Ⅱ)结合函数的奇偶性,分别求出各个区间上的函数解析式,综合得出结论;
(Ⅲ)通过讨论λ的范围,结合函数的单调性,从而得出结论.
解答:
解:(Ⅰ)设f(x)=a(x-h)2+k,(a≠0),
由题意得:
,
解得:k=-1,h=-1,a=1,
∴f(x)=x2+2x;
(Ⅱ)∵y=F(x),x∈R为奇函数,∴F(0)=0,
当x<0时,-x>0,∴F(-x)=f(-x)=x2-2x,
又F(-x)=-F(x),∴F(x)=-x2+2x,
∴F(x)=
;
(Ⅲ)g(x)=(1-λ)x2-(2+2λ)x+1,
若1-λ=0即λ=1,g(x)在[-1,1]递减,
若λ≠1,则对称轴x=
,g(x)在[-1,1]递减,
只需
或
,解得:0≤λ<1,
若λ>1,g(x)在[-1,1]递减,
综上,λ≥0.
由题意得:
|
解得:k=-1,h=-1,a=1,
∴f(x)=x2+2x;
(Ⅱ)∵y=F(x),x∈R为奇函数,∴F(0)=0,
当x<0时,-x>0,∴F(-x)=f(-x)=x2-2x,
又F(-x)=-F(x),∴F(x)=-x2+2x,
∴F(x)=
|
(Ⅲ)g(x)=(1-λ)x2-(2+2λ)x+1,
若1-λ=0即λ=1,g(x)在[-1,1]递减,
若λ≠1,则对称轴x=
| 1+λ |
| 1-λ |
只需
|
|
若λ>1,g(x)在[-1,1]递减,
综上,λ≥0.
点评:本题考查了二次函数的性质,考查了求函数解析式问题,考查了分类讨论思想,是一道中档题.

练习册系列答案
相关题目
在球面上有四点P、A、B、C,如果PA、PB、PC两两垂直,且PA=PB=PC=a,则这个球的表面积是( )
| A、3πa2 |
| B、4πa2 |
| C、5πa2 |
| D、6πa2 |
下列各组中两个函数是同一函数的是( )
A、f(x)=
| ||||||
B、f(x)=x g(x)=
| ||||||
| C、f(x)=1 g(x)=x0 | ||||||
D、f(x)=
|
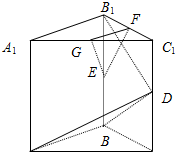 在直三棱柱ABCA1B1C1中,∠ABC=90°,BC=2,CC1=4,点E在线段BB1上,且EB1=1,D,F,G分别为CC1,C1B1,C1A1的中点.求证:
在直三棱柱ABCA1B1C1中,∠ABC=90°,BC=2,CC1=4,点E在线段BB1上,且EB1=1,D,F,G分别为CC1,C1B1,C1A1的中点.求证: