题目内容
15.已知向量$\overrightarrow{BA}$=(1,$\sqrt{3}$),$\overrightarrow{BC}$=(2,0),(1)求∠BAC的大小
(2)求向量$\overrightarrow{BA}$在向量AC方向上的投影.
分析 (1)先求出$\overrightarrow{AB}$、$\overrightarrow{AC}$的坐标,利用两个向量的数量积的定义,求得∠BAC的大小.
(2)根据一个向量在另一个向量上的投影的定义,求得向量$\overrightarrow{BA}$在向量AC方向上的投影.
解答 解:(1)∵向量$\overrightarrow{BA}$=(1,$\sqrt{3}$),$\overrightarrow{BC}$=(2,0),
∴$\overrightarrow{AB}$=(-1,-$\sqrt{3}$),$\overrightarrow{AC}$=$\overrightarrow{AB}+\overrightarrow{BC}$=(1,-$\sqrt{3}$)
∴cos∠BAC=$\frac{\overrightarrow{AB}•\overrightarrow{AC}}{|\overrightarrow{AB}|•|\overrightarrow{AC}|}$=$\frac{-1+3}{2•2}$=$\frac{1}{2}$,∴∠BAC=$\frac{π}{3}$.
(2)向量$\overrightarrow{BA}$在向量AC方向上的投影为|$\overrightarrow{BA}$|•cos(π-∠BAC)=2(-cos∠BAC)=2•(-$\frac{1}{2}$)=-1.
点评 本题主要考查两个向量的数量积的定义,求一个向量在另一个向量上的投影,属于中档题.

练习册系列答案
相关题目
7.现有10支队伍参加篮球比赛,规定:比赛采取单循环比赛制,即每支队伍与其他9支队伍各比赛一场;每场比赛中,胜方得2分,负方得0分,平局双方各得1分.下面关于这10支队伍得分的叙述正确的是( )
| A. | 可能有两支队伍得分都是18分 | B. | 各支队伍得分总和为180分 | ||
| C. | 各支队伍中最高得分不少于10分 | D. | 得偶数分的队伍必有偶数个 |
4.已知向量$\overrightarrow a=(x,-1)$,$\overrightarrow b=(1,\sqrt{3})$,若$\overrightarrow a⊥\overrightarrow b$,则$|\overrightarrow a|$=( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 4 |
7.已知P(B|A)=$\frac{3}{10}$,P(A)=$\frac{1}{5}$,P(B)=$\frac{2}{3}$,则P(AB)=( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{5}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{50}$ |
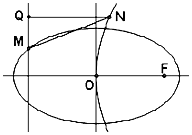 椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上有一点M(-4,$\frac{9}{5}$)在抛物线y2=2px(p>0)的准线l上,抛物线的焦点也是椭圆焦点.
椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上有一点M(-4,$\frac{9}{5}$)在抛物线y2=2px(p>0)的准线l上,抛物线的焦点也是椭圆焦点.