题目内容

10．函数y=$\frac{x^2}{{{2^x}-2}}$的图象大致是（　　）
A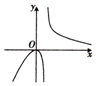．B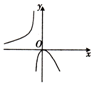．C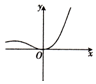．D．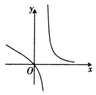

分析 根据函数的定义域与函数值的符号进行判断．

解答 解：由函数有意义得2x-2≠0，即x≠1，排除B，C；
当x＜0时，y=$\frac{{x}^{2}}{{2}^{x}-2}＜0$，排除D；
故选A．

点评 本题考查了函数图象的判断，一般从定义域、值域、特殊点、单调性等方面进行判断，属于基础题．

练习册系列答案
相关题目
20．等差数列{an}的公差d≠0，且a3，a5，a15成等比数列，若a5=5，Sn为数列{an}的前n项和，则数列{$\frac{{S}_{n}}{n}$}的前n项和取最小值时的n为（　　）
A．3B．3或4C．4或5D．5
1．若x，y满足$\left\{\begin{array}{l}{y-1≥0}\\{x-y+1≥0}\\{x-1≤0}\end{array}\right.$，则x+y的最小值是（　　）
A．-1B．1C．2D．3
18．过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左焦点F1作斜率为1的直线，分别与渐近线相交于A，B两点，若$\frac{|A{F}_{1}|}{|B{F}_{1}|}$=$\frac{1}{2}$，则双曲线的离心率为$\sqrt{10}$．
5．已知函数f（x）=-x3+ax2-x-2在（-∞，+∞）上是单调函数，则实数a的取值范围是（　　）
A．（-∞，-$\sqrt{3}$）∪（$\sqrt{3}$，+∞）B．（-$\sqrt{3}$，$\sqrt{3}$）C．（-∞，-$\sqrt{3}$]∪[$\sqrt{3}$，+∞）D．[-$\sqrt{3}$，$\sqrt{3}$]
15．已知向量$\overrightarrow{BA}$=（1，$\sqrt{3}$），$\overrightarrow{BC}$=（2，0），
（1）求∠BAC的大小
（2）求向量$\overrightarrow{BA}$在向量AC方向上的投影．
2．若sinθ＞cosθ，且tanθ＜0，则角θ的终边位于（　　）
A．第一象限B．第二象限C．第三象限D．第四象限
19．使函数f（x）=$\root{3}{{x}^{2}（1-{x}^{2}）}$满足罗尔定理条件的区间是（　　）
A．[0，1]B．[-1，1]C．[-2，2]D．[-$\frac{3}{5}$，$\frac{4}{5}$]
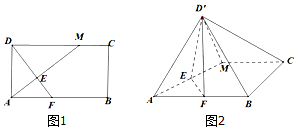2．如图，在矩形ABCD中，AB=2BC，点M在边CD上，点F在边AB上，且DF⊥AM，垂足为E，若将△ADM沿AM折起，使点D位于D′位置，连接D′B，D′C，得四棱锥D′-ABCM．
（1）求证：平面D′EF⊥平面AMCB；
（2）若∠D′EF=$\frac{π}{3}$，直线D′F与平面ABCM所成角的大小为$\frac{π}{3}$，求几何体A-D′EF的体积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网