题目内容
7.现有10支队伍参加篮球比赛,规定:比赛采取单循环比赛制,即每支队伍与其他9支队伍各比赛一场;每场比赛中,胜方得2分,负方得0分,平局双方各得1分.下面关于这10支队伍得分的叙述正确的是( )| A. | 可能有两支队伍得分都是18分 | B. | 各支队伍得分总和为180分 | ||
| C. | 各支队伍中最高得分不少于10分 | D. | 得偶数分的队伍必有偶数个 |
分析 对4个选项分别进行判断,即可得出结论.
解答 解:设每支队伍胜x场,负y场,平z场(x,y,z都是不大于9的自然数),则x+y+z=9,且最终得分为n=2x+z;
对于A,某支队伍得分18分为满分,也就是胜了9场,那么其他9队至少有一次负,就不可能再得18分,故错误;
对于B,总共要进行${C}_{10}^{2}$=45场比赛,每场比赛的得分和都是2分,最后总得分=45×2=90分,故错误;
对于C,最高得分可能超过10分,比如A中可能为18分,故错误;
对于D,由B可知,各个队伍得分总和m1+m2+…+m10=90,这10个数中,若有(2k+1)个偶数,则有10-(2k+1)=(9-2k)个奇数,其和必为奇数,不可能等于90,∴这10个数中,有偶数个偶数,正确.
故选D.
点评 本题考查合情推理,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
2.若sinθ>cosθ,且tanθ<0,则角θ的终边位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
19.使函数f(x)=$\root{3}{{x}^{2}(1-{x}^{2})}$满足罗尔定理条件的区间是( )
| A. | [0,1] | B. | [-1,1] | C. | [-2,2] | D. | [-$\frac{3}{5}$,$\frac{4}{5}$] |
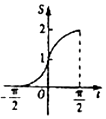
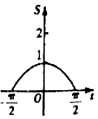
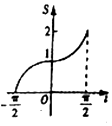
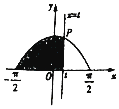 在函数y=cosx,$x∈[{-\frac{π}{2},\frac{π}{2}}]$的图象上有一点P(t,cost),若该函数的图象与x轴、直线$x=-\frac{π}{2},x=t$,围成图形(如图阴影部分)的面积为S,则函数S=g(t)的图象大致是( )
在函数y=cosx,$x∈[{-\frac{π}{2},\frac{π}{2}}]$的图象上有一点P(t,cost),若该函数的图象与x轴、直线$x=-\frac{π}{2},x=t$,围成图形(如图阴影部分)的面积为S,则函数S=g(t)的图象大致是( )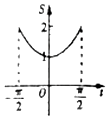
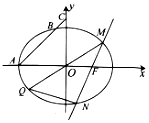 已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左顶点为A,右焦点为F(1,0),过点A且斜率为1的直线交椭圆E于另一点B,交y轴于点C,$\overrightarrow{AB}=6\overrightarrow{BC}$.
已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左顶点为A,右焦点为F(1,0),过点A且斜率为1的直线交椭圆E于另一点B,交y轴于点C,$\overrightarrow{AB}=6\overrightarrow{BC}$.