题目内容
不等式(x-1)(x-2)≥0的解集等于( )
| A、{x|1≤x≤2} |
| B、{x|x≥2或x≤1} |
| C、{x|1<x<2} |
| D、{x|x>1或x<2} |
考点:一元二次不等式的解法
专题:不等式的解法及应用
分析:由对应二次函数和二次方程可得不等式的解集.
解答:
解:∵二次函数y=(x-1)(x-2)的图象开口向上,
又∵二次方程(x-1)(x-2)=0的两根为1和2,
∴不等式(x-1)(x-2)≥0的解集为:{x|x≥2或x≤1},
故选:B
又∵二次方程(x-1)(x-2)=0的两根为1和2,
∴不等式(x-1)(x-2)≥0的解集为:{x|x≥2或x≤1},
故选:B
点评:本题考查一元二次不等式的解集,利用三个二次的关系是解决问题的关键,属基础题.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
若函数f(x)=2-|x|-c的图象与x轴有公共点,则实数c的职值范围是( )
| A、[一1,0) |
| B、[0,1] |
| C、(0,1] |
| D、[1,+∞) |
如图的程序运行后,输出a的值是( )


| A、8 | B、7 | C、6 | D、4 |
若函数y=ax+b-1(a>0且a≠1)的图象不经过第一象限,则有( )
| A、a>1且b≤0 |
| B、a>1且b≤1 |
| C、0<a<1且b≤0 |
| D、0<a<1且b≤1 |
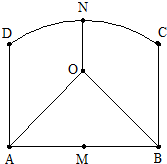 为丰富农村业余文化生活,决定在A,B,N三个村子的中间地带建造文化中心.通过测量,发现三个村子分别位于矩形ABCD的两个顶点A,B和以边AB的中心M为圆心,以MC长为半径的圆弧的中心N处,且AB=8km,BC=4
为丰富农村业余文化生活,决定在A,B,N三个村子的中间地带建造文化中心.通过测量,发现三个村子分别位于矩形ABCD的两个顶点A,B和以边AB的中心M为圆心,以MC长为半径的圆弧的中心N处,且AB=8km,BC=4