ĢāÄæÄŚČŻ
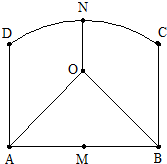 ĪŖ·įø»Å©“åŅµÓąĪÄ»ÆÉś»ī£¬¾ö¶ØŌŚA£¬B£¬NČżøö“å×ÓµÄÖŠ¼äµŲ“ų½ØŌģĪÄ»ÆÖŠŠÄ£®Ķعż²āĮ棬·¢ĻÖČżøö“å×Ó·Ö±šĪ»ÓŚ¾ŲŠĪABCDµÄĮ½øö¶„µćA£¬BŗĶŅŌ±ßABµÄÖŠŠÄMĪŖŌ²ŠÄ£¬ŅŌMC³¤ĪŖ°ė¾¶µÄŌ²»”µÄÖŠŠÄN“¦£¬ĒŅAB=8km£¬BC=4
ĪŖ·įø»Å©“åŅµÓąĪÄ»ÆÉś»ī£¬¾ö¶ØŌŚA£¬B£¬NČżøö“å×ÓµÄÖŠ¼äµŲ“ų½ØŌģĪÄ»ÆÖŠŠÄ£®Ķعż²āĮ棬·¢ĻÖČżøö“å×Ó·Ö±šĪ»ÓŚ¾ŲŠĪABCDµÄĮ½øö¶„µćA£¬BŗĶŅŌ±ßABµÄÖŠŠÄMĪŖŌ²ŠÄ£¬ŅŌMC³¤ĪŖ°ė¾¶µÄŌ²»”µÄÖŠŠÄN“¦£¬ĒŅAB=8km£¬BC=4| 2 |
| 2 |
£Ø1£©ČōČżĢõµĄĀ·½ØÉčµÄ·ŃÓĆĻąĶ¬£¬ĒóøĆĪÄ»ÆÖŠŠÄĄėN“åµÄ¾ąĄė£»
£Ø2£©Čō½ØÉč×Ü·ŃÓĆ×īÉŁ£¬ĒóøĆĪÄ»ÆÖŠŠÄĄėN“åµÄ¾ąĄė£®
æ¼µć£ŗŗÆŹżÄ£ŠĶµÄŃ”ŌńÓėÓ¦ÓĆ
×ØĢā£ŗÓ¦ÓĆĢā,ŗÆŹżĖ¼Ļė,ŗÆŹżµÄŠŌÖŹ¼°Ó¦ÓĆ
·ÖĪö£ŗ£Ø1£©Éč”ĻAOB=¦Č£¬ČżĢõµĄĀ·½ØÉčµÄ·ŃÓĆĻąĶ¬£¬Ōņ
”Į
a=(4
-4tan¦Č)a£¬ĄūÓĆČż½Ē±ä»»Ēó½ā£®
£Ø2£©×Ü·ŃÓƦŲ=2”Į
+a(4
-4tan¦Č)£¬¦Č”Ź[0£¬
]£¬¼“¦Ų=
a+4
a£¬Ēóµ¼ÅŠ¶Ļ¼«Öµµć£¬Įī¦Ų”ä=
a=0£¬µĆsin¦Č=
£¬ŌŁ×Ŗ»»ĪŖČż½Ē±ä»»ĒóÖµ½ā¾ö£®
| 4 |
| cos¦Č |
| 2 |
| 3 |
£Ø2£©×Ü·ŃÓƦŲ=2”Į
4
| ||
| cos¦Č |
| 3 |
| ¦Š |
| 3 |
8
| ||
| cos¦Č |
| 3 |
8
| ||
| cos2¦Č |
| ||
| 4 |
½ā“š£ŗ
½ā£ŗ£Ø1£©²»·ĮÉč”ĻAOB=¦Č£¬ŅĄĢāŅāµĆ¦Č”Ź[0£¬
]£¬
ĒŅMC=4
£¬ÓÉAO=BO=4
=
£¬NO=4
-4tan¦Č£¬
ČōČżĢõµĄĀ·½ØÉčµÄ·ŃÓĆĻąĶ¬£¬Ōņ
”Į
a=(4
-4tan¦Č)a
ĖłŅŌsin(
-¦Č)=
£¬ĖłŅŌ¦Č=
£®
Óɶž±¶½ĒµÄÕżĒŠ¹«Ź½µĆ£¬tan¦Č=tan
=2-
¼“NO=8
-8£¬
“š£ŗøĆĪÄ»ÆÖŠŠÄĄėN“åµÄ¾ąĄėĪŖ(8
-8)km£®
£Ø2£©×Ü·ŃÓƦŲ=2”Į
+a(4
-4tan¦Č)£¬¦Č”Ź[0£¬
]
¼“¦Ų=
a+4
a£¬
Įī¦Ų”ä=
a=0£¬µĆsin¦Č=
µ±0”Üsin¦Č”Ü
2£¬¦Ų”䣼0£¬µ±
£¼sin¦Č”Ü
Ź±£¬¦Ų”䣾0£¬
ĖłŅŌµ±sin¦Č=
Ź±£¬¦ŲÓŠ×īŠ”Öµ£¬
ÕāŹ±£¬tan¦Č=
£¬NO=4
-
“š£ŗøĆĪÄ»ÆÖŠŠÄĄėN“åµÄ¾ąĄėĪŖ(4
-
)km£®
| ¦Š |
| 3 |
ĒŅMC=4
| 3 |
| 3 |
| 4 |
| cos¦Č |
| 3 |
ČōČżĢõµĄĀ·½ØÉčµÄ·ŃÓĆĻąĶ¬£¬Ōņ
| 4 |
| cos¦Č |
| 2 |
| 3 |
ĖłŅŌsin(
| ¦Š |
| 3 |
| ||
| 2 |
| ¦Š |
| 12 |
Óɶž±¶½ĒµÄÕżĒŠ¹«Ź½µĆ£¬tan¦Č=tan
| ¦Š |
| 12 |
| 3 |
¼“NO=8
| 3 |
“š£ŗøĆĪÄ»ÆÖŠŠÄĄėN“åµÄ¾ąĄėĪŖ(8
| 3 |
£Ø2£©×Ü·ŃÓƦŲ=2”Į
4
| ||
| cos¦Č |
| 3 |
| ¦Š |
| 3 |
¼“¦Ų=
8
| ||
| cos¦Č |
| 3 |
Įī¦Ų”ä=
8
| ||
| cos2¦Č |
| ||
| 4 |
µ±0”Üsin¦Č”Ü
| ||
| 4 |
| ||
| 4 |
| ||
| 2 |
ĖłŅŌµ±sin¦Č=
| ||
| 4 |
ÕāŹ±£¬tan¦Č=
| ||
| 7 |
| 3 |
4
| ||
| 7 |
“š£ŗøĆĪÄ»ÆÖŠŠÄĄėN“åµÄ¾ąĄėĪŖ(4
| 3 |
4
| ||
| 7 |
µćĘĄ£ŗ±¾Ģā×ŪŗĻæ¼²éĮĖŗÆŹżµÄŠŌÖŹŌŚŹµ¼ŹĪŹĢāÖŠµÄÓ¦ÓĆ£¬×Ŗ»»ĪŖČż½ĒŗÆŹż×īÖµĒó½ā£®

Į·Ļ°²įĻµĮŠ“š°ø
 ĆūŠ£æĪĢĆĻµĮŠ“š°ø
ĆūŠ£æĪĢĆĻµĮŠ“š°ø
Ļą¹ŲĢāÄæ
ŅŌĻĀŗÆŹżŌŚRÉĻŹĒ¼õŗÆŹżµÄŹĒ£Ø””””£©
| AӢy=-x2 | ||
BӢy=log
| ||
CӢy=
| ||
DӢy=(
|
Čōf£Ø2x+1£©=x2-1£¬Ōņf£Ø0£©=£Ø””””£©
AӢ-
| ||
| BӢ0 | ||
CӢ
| ||
| DӢ-1 |
²»µČŹ½£Øx-1£©£Øx-2£©”Ż0µÄ½ā¼ÆµČÓŚ£Ø””””£©
| AӢ{x|1ӆxӆ2} |
| B”¢{x|x”Ż2»ņx”Ü1} |
| C”¢{x|1£¼x£¼2} |
| D”¢{x|x£¾1»ņx£¼2} |