Question

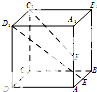已知点E，F分别是正方体ABCD-A₁B₁C₁D₁的棱AB，AA₁的中点，点M，N分别是线段D₁E与C₁F上的点，则与平面ABCD垂直的直线MN有（　　）

• A、0条
• B、1条
• C、2条
• D、无数条

Answer 1

考点：直线与平面垂直的判定

专题：空间位置关系与距离

分析：设正方体ABCD-A₁B₁C₁D₁的棱长为2，以C为原点建立空间直角坐标系，利用向量法求出与平面ABCD垂直的直线MN只有1条．

解答： 解：设正方体ABCD-A₁B₁C₁D₁的棱长为2，
以C为原点建立空间直角坐标系，
则D₁（2，0，2），E（1，2，0），

D1E

=（-1，2，-2），
C₁（0，0，2），F（2，2，1），

C1F

=（2，2，-1），
设

D1M

=λ

DE

，则M（2-λ，2λ，2-2λ），
设

C1N

=t

C1F

，则N（2t，2t，2-t），
∴

MN

=（2t-2+λ，2t-2λ，2λ-t），
∵直线MN与平面ABCD垂直，
∴

2t-2+λ=0 2t-2λ=0 2λ-t≠0

，解得λ=t=

2

3

，
∵方程组只有唯一的一组解，
∴与平面ABCD垂直的直线MN有1条．
故选：B．

点评：本题考查空间直线与平面的位置关系，主要是直线与平面平行的判断和面面平行的判定与性质，考查空间想象能力和简单推理能力．