题目内容
设曲线y=x2-2x-4lnx的一条切线的斜率小于0,则切点的横坐标的取值范围是( )
| A、(-1,2) |
| B、(-1,0)∪(2,+∞) |
| C、(0,2) |
| D、(0,+∞) |
考点:利用导数研究曲线上某点切线方程
专题:计算题,导数的概念及应用
分析:求导数,令其小于0,结合函数的定义域,即可求出切点的横坐标的取值范围.
解答:
解:设切线的切点为(x,y),
∵y=x2-2x-4lnx,
∴y′=2x-2-
<0,
∵x>0,
∴x2-x-2<0
∴0<x<2,
故选:C.
∵y=x2-2x-4lnx,
∴y′=2x-2-
| 4 |
| x |
∵x>0,
∴x2-x-2<0
∴0<x<2,
故选:C.
点评:考查了利用导数求曲线上过某点切线方程的斜率,考查了基本初等函数的导数公式,是中档题.

练习册系列答案
相关题目
函数f(x)=|sin2x+cos2x|的最小正周期为( )
A、
| ||
| B、π | ||
C、
| ||
| D、2π |
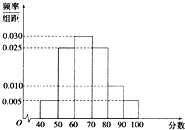 某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分成6组:[40、50),[50、60),[60、70),[70、80),[80、90),[90、100]加以统计,得到如图所示的频率分布直方图.已知高一年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为( )
某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分成6组:[40、50),[50、60),[60、70),[70、80),[80、90),[90、100]加以统计,得到如图所示的频率分布直方图.已知高一年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为( )| A、588 | B、420 |
| C、450 | D、120 |
执行如图所示的程序框图,输出的S值为( )


| A、1 | B、5 | C、14 | D、30 |
设f(x)=3x-x2,则在下列区间中,使函数f(x)有零点的区间是( )
| A、(0,1) |
| B、(1,2) |
| C、(-1,0 ) |
| D、(-2,-1) |
执行如图所示的程序框图,若输入的x值为
,则输出的y的值为( )

| 1 |
| 2 |

| A、1 | ||
| B、-1 | ||
C、
| ||
D、
|
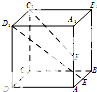 已知点E,F分别是正方体ABCD-A1B1C1D1的棱AB,AA1的中点,点M,N分别是线段D1E与C1F上的点,则与平面ABCD垂直的直线MN有( )
已知点E,F分别是正方体ABCD-A1B1C1D1的棱AB,AA1的中点,点M,N分别是线段D1E与C1F上的点,则与平面ABCD垂直的直线MN有( )