题目内容
将一个两位数的两个数字左右顺序颠倒(要求颠倒后仍是一个两位数),将所得到的数和原数相加,若和中没有一个数字是偶数,则称这个数是奇和数.在所有的两位数中,奇和数的个数为( )
| A、20 | B、24 | C、32 | D、40 |
考点:计数原理的应用
专题:排列组合
分析:因为和中没有一个数字是偶数,只有奇数加偶数和是奇数,故两位数是一个奇数和一个偶数组成,
解答:
解:由题意知,两位数是一个奇数和一个偶数组成,有
•
•
=40个,
所得到的数和原数相加共有不同奇和数为
=20.
故选:A.
| C | 1 5 |
| C | 1 4 |
| A | 2 2 |
所得到的数和原数相加共有不同奇和数为
| 40+40 |
| 4 |
故选:A.
点评:本题考查了排列组合的数字问题,审清题意,找到两位数是一个奇数和一个偶数组成是关键,属于中档题.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
函数f(x)=|sin2x+cos2x|的最小正周期为( )
A、
| ||
| B、π | ||
C、
| ||
| D、2π |
执行如图所示的程序框图,输出的S值为( )


| A、1 | B、5 | C、14 | D、30 |
cos
的值为( )
| 23π |
| 6 |
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
 如图是甲、乙两名同学在五场篮球比赛中得分情况的茎叶图,那么甲、乙两人和分的标准差s甲
如图是甲、乙两名同学在五场篮球比赛中得分情况的茎叶图,那么甲、乙两人和分的标准差s甲
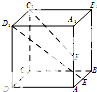 已知点E,F分别是正方体ABCD-A1B1C1D1的棱AB,AA1的中点,点M,N分别是线段D1E与C1F上的点,则与平面ABCD垂直的直线MN有( )
已知点E,F分别是正方体ABCD-A1B1C1D1的棱AB,AA1的中点,点M,N分别是线段D1E与C1F上的点,则与平面ABCD垂直的直线MN有( )